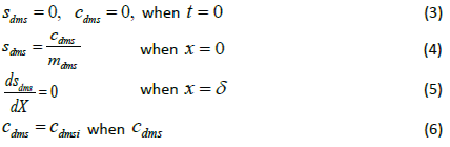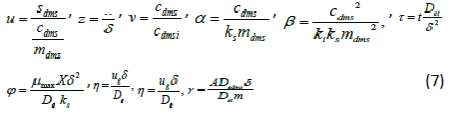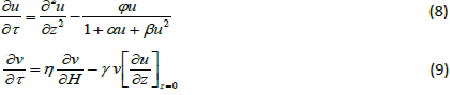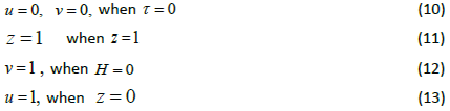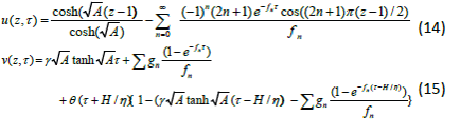Keywords
|
| Mathematical modeling, New Homotopy perturbation method, Nonlinear equation, Biofilter, Dimethyl sulphide. |
INTRODUCTION
|
| A biofilteration system was designed using mature composts of municipal solid waste mixed with pruning residues as packing materials to treat vapours of α-pinene [1]. Lee et al. [2] described the cleaning of a waste gas stream using bench scale biofilters or bio trickling filters. Bhat et al. [3] describe the differential evolution method for efficient parameter estimation in biofilter modelling. Baquerizo et al. [4] developed a dynamic model to describe ammonia removal in a gas-phase biofilter. The mathematical model is based on discretized mass balances and detailed nitrification kinetics that include inhibitory effects caused by free ammonia and free nitrous acid. A bench scale biofilter packed with compost and wood chips on with potential DMS degrading culture could efficiently remove DMS from ambient air. Further, the same biofilter operated for the treatment of vent gas generated from a P&P industry indicated DMS removal [5]. Trevena [6] presents concentrations of dimethylsulphide (DMS) and its precursor compound dimethylsulphoniopropionate in a variety of sea ice and seawater habitats in the Antarctic Sea Ice Zone during spring and summer. Biofilters are applied for odour reduction, but their operational control was limited. Dimethyl sulphide elimination depends up on the DMS inlet concentration, gas residence time, and membrane polymer [7]. Yea et al. [8] studied the effect of electropulsing ultrasonic shock (EUS) on the microhardness and microstructure of Ti6Al4V alloy. The effects of high-energy electropulsing treatment (EPT) on the microhardness and corrosion behavior of the surface gradient oxide coating on the titanium alloy matrix were investigated using infrared thermoscope, micro-hardness, three-dimensional optical microscope, electrochemical work station, scanning electron microscope equipped with electron backscatter diffraction, X-ray Diffraction, Fourier Transform Infrared Spectroscopy and Thermogravimetryanalyzer [9]. |
| Recently Giri and Pandey [10] developed a mathematical model of bench scale biofilter packed with compost and wood chips. However to the best of our knowledge, no analytical expression of concentration of dimethyl sulphide in the gas phase and in the biofilm phase have been reported. The purpose of this communication is to drive the approximate analytical expression for the dimethyl sulphide concentration in both the phase using the new Homotopyperturbation method. |
|
Mathematical formation of the problem
|
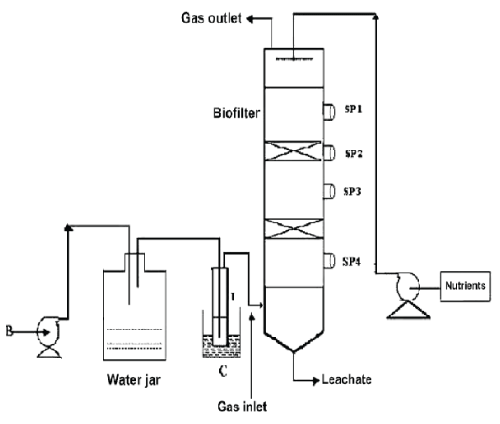
| The schematic of the experimental setup of the air phase biofilter for treatment of water gas containing DMS is shown in the Figure 1. The nonlinear differential equations describing the removal of DMS from waste gas in a differential section of the biofilter can be represented as [10] |
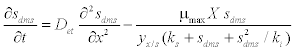 (1) (1) |
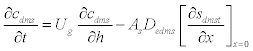 (2) (2) |
| where μmax is the maximum specific growth rate, s k is the half saturation constant, yx/s is the biomass yield coefficient, Det is the effective diffusion coefficient of the DMS in the biofilm, sdms represents the liquid phase concentration of DMS in biofilm and X is the position in the biofilm. x represents the overall population of microorganisms that includes specific DMS degrading microorganisms. dms c is DMS concentration in gas phase and mdms is the air/biofilm partition coefficient. g U is superficial gas velocity, s A is the biofilm surface area and h is position along the biofilter.. The initial and boundary conditions for above equation can be represented as |
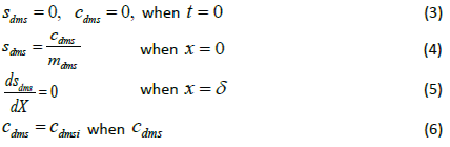 |
| where dms c is the DMS concentration in gas phase, dms m is the air/ biofilm partition coefficient and i represents conditions at the inlet of the biofilter. |
|
Dimensionless form of the problem
|
| To compare the analytical results with simulation results, we make the above non-linear partial differential equations (1) and (2) in dimensionless form by defining the following parameters: |
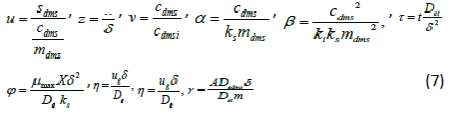 |
| The equations (1) and (2) reduce to the following dimensionless form: |
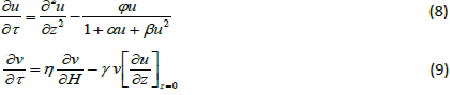 |
| whereu and v represents the dimensionless concentration of DMS in the biofilm phase and in the gas phase, α andβ are saturation parameters. Now the initial and boundary conditions may be presented as follows [10]: |
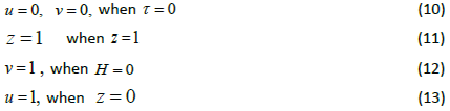 |
|
Analytical expression for the dimensionless concentrations of DMS in the biofilm phase and in the gas phase for all values of parameter
|
| Homotopy perturbation method is applied to solve the nonlinear two-dimensional wave equation. The analytic solution of the nonlinear wave equation is calculated in the form of a series with easily computable components [11]. Hu et al. [12] investigated the anaerobic digestion kinetics of ice cream water waste using Monod and Contois models. He used the HPM to solve the Lighthill equation [13], the Diffusing equation [14] and the Blasius equation [15]. The idea has been used to solve nonlinear boundary value problems, integral equations and many other problems. The Homotopy perturbation method [16-18] is very effective and simple. The HPM is unique in its applicability, accuracy, efficiency uses the imbedding parameter p as a small parameter and only a few iterations are needed to search for asymptotic solutions. Using Laplace transform technique and new Homotopy perturbation method (Appendix A) we can obtain the concentration of DMS in the biofilm phase and the gas phase as follows: |
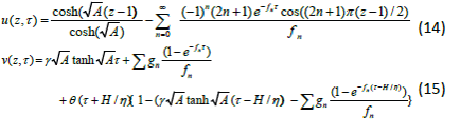 |
| where |
 |
|
Numerical simulation
|
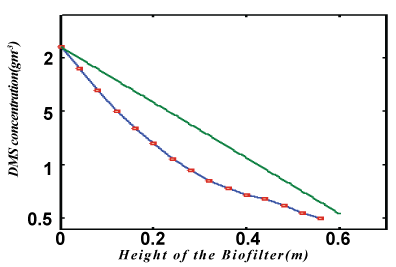
| The non-linear differential equations (1) and (2), are also solved using numerical methods(Matlab). The function pdex4 in Matlab software which is the function of solving the boundary value problems for ordinary differential is used to solve this equation. The function pdepe (Finite element method) in Matlab software which is a function of solving the initial-boundary value problems is used to solve Eqs. (8) and (9). The analytical solution of DMS concentrations in biofilm phase are compared with simulation results in Figure 2. A satisfactory agreement is noted. The Matlab program is also given in Appendix B. |
Results and Discussions
|
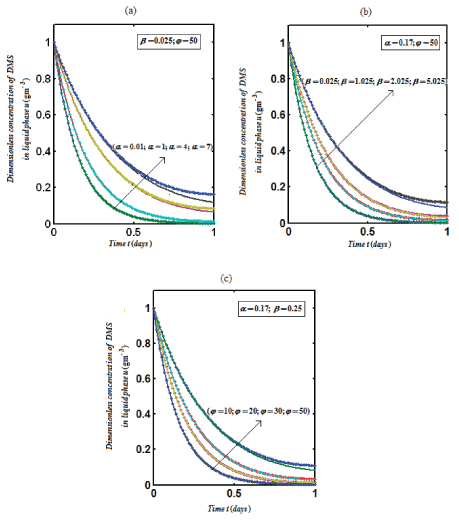
| Eqns. (14) and (15) represent the simple analytical expressions pertaining to the DMS concentration in the gas phase and the biofilm phase respectively. The main variable of interest in this study is the concentration of DMS in the biofilm phaseu and gas phase v . The concentration of dimethyl sulphide in the gas phase depend on the following three factorsα ,β and? The parameter ? depends upon specific surface area of the biofilm s A , effective diffusion coefficient in the biofilm e D , and superficial gas velocity g U. The parameter α depends upon the biofilm thicknessδ and β depends on inlet DMS concentration. |
| Figure 2 represents the concentration of DMS in the biofilm phase u versus time α ,β for different values of α ,β and ? . From Figures 1a-1c, it is inferred that the concentration of DMS increases when α ,β and ? increases for some fixed values of other parameters. |
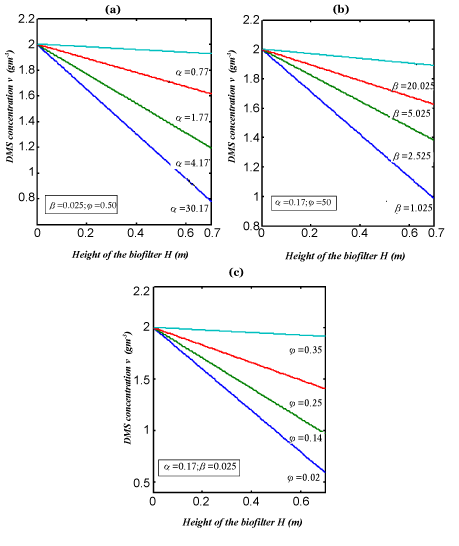
| In Figure 3, the concentration of DMS in the gas phase v versus height H for various values of parameter are plotted. From these figures it is observed that the result is compared with the concentration of v increases with the decrease of α ,? and the increase of β . In Figure 4. The experimental analytical (simulation) results for DMS removal ration for some fixed values of the parameter. A satisfactory argument is noted. |
Conclusion
|
| We have presented a theoretical model of bench scale biofilter packed with compost and wood chips seeded with DMS degrading micro organisms. A nonlinear time dependent differential equations in bench-scale biofilter has been solved analytically. Approximate analytical expressions pertaining to the concentration of DMS in the gas phase and biSofilm phase for all values of the parameters are obtained using the new Homotopy perturbation method. This analytical result helps for the better understanding of the model. Our results are compared with the numerical simulations and it gives satisfactory agreement. |
Acknowledgements
|
| This work was supported by the DST SB/SI/PC-50/2012, New Delhi, India. The authors are thankful to Dr. Murali, The Principal, The Madura College, Madurai, and The Secretary, The Madura College Board, Madurai for their encouragement. |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|





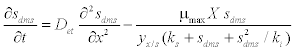 (1)
(1)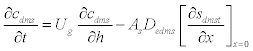 (2)
(2)