Keywords
Action selection; Winner-take-all instabilities; Risky behavior; Recognition automata; Edelman’s ‘Darwin’ series; Markram’s blue brain project; Non-shannon notturing computable functions
Introduction
The study of decision making has relevance for varied fields as neuroscience, psychology, economics, statistics, political science, and computer science [1]. For beginning of the choice process is important a phenomenon of selective attention as an early mechanism for action selection reducing the volume of information transformed into action-related representations. In this connection, neurophysiological evidence for the modulation of fronto-parietal activity by decision factors is very strong. Recent studies on decision making show, that lateral intraparietal area (LIP) activity correlates not only with sensory and motor variables, but also with decision variables as expected utility, local income, hazard rate and relative subjective desirability.
The prefrontal cortex (PFC) is also strongly involved in decision making. The PFC is not a homogenous system but a diverse collection of specialized regions. Here we hypothesize no exclusivity of ‘winner’s-take-all’ strategies in choice processes. Instead, prefrontal regions evolve through the collection of votes for selecting actions in more abstract and complex decisions [2]. It has been shown how to map linear localist decision networks into computationally equivalent distributed decision networks, and derived the parameters of decision networks with distributed representations [3].
Materials and Methods
In this paper we are using comparison via a semi-analytical approach of biologically realistic neural models with so-called sequential sampling models to show existing deficits in these models caused by biological constraints. The existing models of decision making based on neurophysiological data outgoing from cortical connections encoding the stimulus-response mapping. The firing rate represents the information on which the developing decision is made.
The tool is an action selection as the resolution of conflict between command centers in the brain competing for behavioral expression [4]. Competition between brain centers for expression reassessed by a central switch controlling the urgency of action request. Due to anatomical and physiological evidence is the basal ganglia hypothesized as the neural substrate for above switch. The basal ganglia receive enough neural input to send tonic inhibition to midbrain, brain stem and thalamus targets during execution of motor actions, also blocking cortical control over given actions. This enables action selection when neurons in the output nuclei have their activity reduced under control of the rest parts of basal ganglia and for this reason disinhibiting their targets.
Decision making between alternative actions, cortical regions integrate evidence and the basal ganglia play a role of the central switch reassessing this evidence and allowing the behavioral requests. Cortical sensory regions respond if their receptive fields meet the stimulus and are tuned for motion [4].
The decision making process is defined by finding which xi(t) has the highest mean, whereas i denote the evidence supporting this decision, provided at time t. The decision can be made when an input decreases its activity below the threshold. Action of basal ganglia outputs can performing selection by disinhibition of target structures.
Problem is that the instantaneous firing rates (for example in middle temporal area-MT during visual task) are noisy while reflecting the uncertainty inherent in stimulus and its neural representation. This noise causing that decisions based on MT neurons would be inaccurate. The reason is that the largest firing rate does not always indicate the direction coherent motion in the stimulus. In similar cases the statistical interpretation is needed.
Within each population, neurons with similar tuning excite each other through reciprocal topological connections, and neurons with dissimilar tuning inhibit each other. Noise is added to all neural activities, what could deform the choice process. These potential actions are represented simultaneously in frontal and parietal cortical regions during sensorimotor processing [2].
In most of the models of decision making, the choices are predefined and represented by distinct populations, one or more per choice. We prefer the stochastic models suggesting that the choices emerge within a population of neurons whose activity represents the probability density function of potential movements.
Decisions based on abstract rules may first be expressed in frontal regions and propagate backward to posterior parietal cortex (PPC). Than, the decisions are proposed to emerge as a ‘distributed consesnsus’, which is reached when a competition of potential actions is unbalanced by the accumulation of evidence in favor of a given choice (s).
Neurobiology of preference reversals
The medial frontal cortex, especially the pre-supplementary motor area (pre-SMA), plays a key role in this behavioral switching process. The pre-SMA switch signal is implemented by the STN through direct connections from the pre-SMA to the subthalamic nucleus (STN). It is interesting that the switchselective activity reflects a neuronal process related to an increased level of arousal, but arousal should not depend on the direction of switching. It could reflect a shift of attention or a direction-selective conflict between automatic and controlled action.
The no-go pathway consists of a direct connection from the STN to the substantia nigra pars reticulata (SNr), which in turn project to the SC. Because STN neurons are excitatory and SNr neurons are inhibitory, activation of STN neurons should result in the suppression of superior colliculus (SC) output neurons. The suppression of ipsiversive movements can be mediated by SNr neurons projection to the SC on the opposite side, and contraversive suppression can be mediated by SNr neurons projecting to the SC on the same side.
The go pathway uses indirect connections from the STN to the SNr through the external segment of the globus pallidus (GPe). Beacause GPe neurons are inhibitory, the effect of the STN output may be reversed from no-go to go type (again ipsilateral go or contralateral go) [5].
Behavioral switching is usually not a local motor phenomenon and requires the switch of mental operations (cognitive strategies). Probably axon collaterals to the nonoculomotor neurons in the GPe and GPi underlie these diverse aspects of behavioral switching.
The probability shift of reversals, repulsions is with a sudden radiative transition of molecule from one vibronic state to another. It illuminates the coupling between individual molecule dynamics and collective degrees of freedom. In a diatomic molecule the nuclei remain at their instantaneous position and keep their momenta during an electronic transition and the intermolecular potential changes suddenly. The radiative dissociation of diatomic molecule may change the binding potential from attractive to repulsive and vice versa. This can lead to a polarization of the intermolecular potential as the basis for overlap and resonance.
One of the options may be an outcome of unsupervised random connections between neurons in the STN, SNr, and GPe. Cortical neurons (pre-SMA neurons) need to be connected appropriately to particular combinations of random connections. The right connection may be achieved by reinforcement learning mechanisms. Dopaminergic innervations of STN neurons might underlie of this plastic mechanism. The switching functions in this area probably extend beyond the motor domain, such as thoughts and emotions.
The ‘winner-take-all’ instabilities
From various models applications we propose that decisionmakers switch their attention stochastically, from dimension to dimension. The evaluation is made for one of the dimensions, and preference is integrated by leaky competing accumulators. Decision-makers show often errors due an over estimative discrepancy between subjective and objective probability. The inhibition antagonism is deforming a trade-off in units of log P probabilities.
To achieve a system to exhibit winner-take-all behavior, the real part of the remaining eigenvalue must be negative to avoid unwanted instabilities. This implies that perturbations along the eigenvector corresponding to the ‘winner-take-all’ instability. The stochastically driven dynamics will lead to leading order with an additive noise. Evolution of activity than can be thought as the motion of a noise-driven, over damped particle in a potential [6].
Reductions of linear connectionists models to the linear diffusion equation lead to a linear term proportional to the difference between intrinsic leak and the effective cross inhibition. Information from the unattended channel often leaks through, thus changing the filter from all-or-none device to an attenuator. Reduced mapping effects with an irrelevant dimension and the attenuation of information transmission through a leaky filter may reflect similar mechanism. The stimulus-response compatibility (SRC) in this task did not have dimensional overlap, the response conflict triggered by the noise stimuli are sufficiently similar in structure. Additive effects were obtained between mapping and the number of alternatives when mapping was waried by altering the rules for the S-R pairings [7].
Setting relatively high thresholds effectively eliminates one free parameter from the model, e. i. the threshold placement. Threshold for detection of a decision in the brain, may be set by downstream areas (superior colliculus, the basal ganglia). The model of flexible sensorimotor mapping in which reward-dependent synaptic plasticity shapes the response output of a winner-take-all decision making circuit [8]. As it can be seen, the winner-take-all instabilities leading to models driven with an additive noise and often to voluntarily selected parameters of the system dynamics.
Decision error catastrophe
The term “error catastrophe” was originally introduced in the theory of molecular evolution [9], and now is fashionable between virologists. It was suggested on the basis of quantitative sequence studies that a common antiviral drug by its mutagenic action drives poliovirus into an error catastrophe of replication, thereby turning a productive action into an abortive one. The molecular indetermination in transition to error catastrophe show the complexity of the mechanism involved in proliferation of informational infection.
A catastrophe is usually triggered if certain limits are exceeded. For replication there is a limiting value of error rate that must be surpassed. This limit is the error threshold. It is caused by the inherent autocatalytic nature of replication, which represents transfer of information. During error catastrophe, the replication provides an exponential proliferation of the information contained in the sequence as a whole. Different sequences competing in a stochastic manner behave as cooperative units.
This nondeterministic fluctuating selection was named as ‘non-Darwinian’ [10,11]. Darwin himself although anticipated this type of selection. Kimura and Ohta’s stochastically fluctuating selection can remind us of critical phase transition.
These phase transitions associated with natural selection do not take place in the space-time coordinates of our physical space. Rather they refer to an abstract information space as a discrete point space with metric named after Hamming [10,12]. The error rate represented by the consensus sequence is conserved up to the error threshold.
For our concept of the decision error catastrophe (DEC) is essential for schizophrenia that the population of master and mutant types changes quite conspicuously bellow the error threshold, but is “all-or-none” above threshold. The decision is now made whenever any output decreases its activity below the threshold. It is in agreement with action of basal ganglia outputs in performing selection by disinhibition of target structures [13].
Threshold mechanism explains the physiological underpinnings of the speed-accuracy trade-off. Thus predicts that increases in common input in to the two populations will lead to faster reactions and poorer performance, while decreases in input will lead to better performance and slower reactions. Increasing the noise amplitude leads also to decreasing performance [6].
We are proposing to see “winner-take-all” strategies as counterproductive, leading through a competition reduction to the thermodynamic losses, but only above the error threshold. The all-or-none nature of the error threshold is first realized after it is crossed. For DEC is also specific that is linked to all functions involved in a given phase of the choice process and could be terminated after lose all its pathogenic information (for example panic information, toxic actives in financial sector, etc.).
Risky behavior modulated by expected reward
Striatal neurons selective for actions are modulated by expected reward. It is also valid for cortical integrators, which are similarly modulated by expected reward. Phasic release of dopamine is associated with urgent or unexpected behavioral events. The phasic dopamine signal represents a variable in temporal difference reinforcement learning, the reward prediction error.
Tonic levels of dopamine influence the speed-accuracy trade-off in making responses (especially the reaction times- RTs). In MSPRT this mechanism play role in finding the speedaccuracy trade-off that maximizes the rate of reward acquisition including repeating sequences of choices [4]. Decision makers can often show an over estimative discrepancy, between subjective and objective probability.
The prefrontal cortex is part of a neuronal circuit playing a central role in fear conditioning and stress responsivity. Poor conditioning is associated with poor development of the conscience and less autonomic responsive persons are aversive to social criticism and may become predisposed to antisocial behavior [14].
The prefrontal cortex is also involved in the regulation of arousal and deficits in autonomic and central nervous system arousal are viewed as facilitating a stimulation-seeking antisocial behavioral response to compensate an under arousal. For the process of decision-making is important that subjects with prefrontal damage fail to give anticipatory autonomic responses to choice risky options and make bad choices even when they are aware of the more advantageous response option.
This inability to reason and decide advantageously in risky situations like financial transactions could be, contribute to the impulsivity, rule breaking and reckless irresponsible behavior making 4 of the 7 traits of APD [15,16].
The prefrontal cortex contribute to the manipulation of the knowledge on which adaptive behavior depend. Only in the right hemisphere impair the ability to make appropriate decisions in the social and financial realms. Particular part of the medial prefrontal cortex: the orbitofrontal cortex on the right hemisphere showed 14,2% less (glucose deficit) activity in subjects with diminished responsivity. Many of them probably fulfill the criteria for Antisocial personal disorder (APD) based primarily on subject’s behavioral histories. Hare’s revised psychopath check-list (PCL-R) is used for assessments of the emotional deficits that underlie diminished responsibility [17].
Randomness is a part of the decision process itself
The model of cortical decision making in area LIP can achieve integration within neuronal pools sharing a common response field (RF) with an inhibitory antagonism between pools representing opposite directions. The criterion controls the trade-off between speed and accuracy in the basal ganglia. Prior probabilities affect the threshold for initiating action.
During the choice process the threshold is changing as linear function of the logarithm of the prior. The decision variable (DV) has units log (P). It is a basis of a form of probabilistic reasoning with the DV representing a level of certainty. The action is initiated when the DV reaches the threshold. Rate of rise is not determined precisely but is rather a random number from a Gaussian distribution. Different decision strategies seem to trade-off in these units of log (P). Tonic levels of dopamine influence the speed-accuracy trade-off in making responses. Evidence is corrupted by noise (9) and reward (3) during trade-off in units of log (P) probabilities. As result, randomness and informational entropy is part of the decision process itself.
Choices in perceptual and value-based decision are governed by randomness. Typical randomness is given by perceptual evidence as a mixture of signal plus noise. For value-based decisions, the randomness is often part of the decision process itself. The decision rule is than a probabilistic random selection. The decision mechanism may generate randomness and reflect a noisy input [1].
Complex decisions are made in a distributed way. The locus of decision lies in the pattern of connections between sensory inputs and motor outputs and may involve numerical errors as well. Transfer entropy (TE) quantifies the deviation from the generalized Markov property:
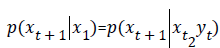
where xt is the bin assignment of time series x at time t. If conditioning of priors at Y1 alters the transition probabilities of  then the assumption of a Markov process is invalid. Incorrectness of assumption expressed by the TE, as the Kullback-Liebler entropy:
then the assumption of a Markov process is invalid. Incorrectness of assumption expressed by the TE, as the Kullback-Liebler entropy:
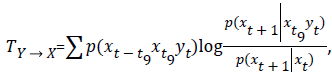
where the index Y X indicates the influence of Y on X. TE is nonsymetric and can detect the directed exchange of information (information flow or causal influence) between x and y [18]. Interpretation by decision rule may increase the degree of noise, what should be a beginning of “the error catastrophe”. Because the evidence is a mixture of signal plus noise and the decision rule is probabilistic.
The basal ganglia as a neurorobot in brain
The cortex may operate as a first stage of a two-stage decision process, making a first pass filter. It is concerning actions with small urgency, thereby preventing these request from propagating to the second stage in the basal ganglia.
Here the globus pallidus (GP) plays a role in limiting subthalamic nuclei (STN) activity via a log transform. In this function GP automatically limits the excitation of basal ganglia output nuclei to allow network mechanisms to perform selection [4].
The basal ganglia also gates access to working memory and decides if a newly presented stimulus should be stored in the working memory. The basal ganglia implementing the multiple sequential probability ratio test (MSPRT), including non-linear processing in STN could also optimize selection in working memory and cognitive selection in general.
STN of the basal ganglia is an important element of motor control. A unique feature of the STN is that it receives inputs directly from the frontal cortex. When a sudden change in the environment requires a cessation of automatic ongoing activity and instead deliberately controlled behavior must be performed, the STN is suitable for quick control of action.
Biological constraints on gains and losses
In many cases decision networks cannot achieve optimal performance due to biological constraints. Information processing in biological neurons is non-linear. It means that all existing neuronal models based on linear processing are not optimal for choice between multiple alternatives.
The firing rate of biological neurons cannot be negative and exceed a certain level due to the refractory period of biological neurons. The nonlinear leaky competing accumulator (LCA) model has also its biological limits. The values of y1 and y2 are transformed through a nonlinear activation function f(y) before they influence (inhibit) each other:
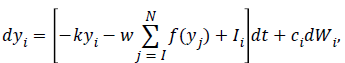
integration starts from yi (0)=0, an input unit with mean activity Ii , and independent white noise fluctuations dWi of amplitude ci . These units also inhibit each other with a connection weight w, k denotes the decay rate of the accumulators activity (leak), N means the number of alternatives.
Performance and dynamics of choice models suggests that in some cases the balance of inhibition and decay is not optimizing the performance, but rather it may be more profitable increase the inhibition parameter w, which increase inhibition of accumulators y3, y4, y5 and thus prevent from the competition with y1 and y2 (for N=5 alternatives) [3]. This type of preemptive discrimination in favor of ‘pointer states’, which is suppressing further competitive behavior, is known from the Quantum Darwinism as a mechanism of “inquisition” [19].
In the nonlinear LCA model there are still questions about leaky accumulation, competition, extent of noisy inputs, integration of noisy evidence represented in the firing rates, etc.
The choice is made when activity of the neuronal population representing one of the alternatives reaches a decision threshold. Neurons in cortical regions as the lateral intraparietal area (LIP) integrate evidence by averaging out the noise allowing the accuracy of choice, but it is only partial in effect. Noisy evidence is leading to inaccurate mutual inhibition of accumulators. In the LCA model accumulator units are leaky integrators, integrates evidence from input units with independent white noise fluctuations of amplitude. These units also inhibit each other by way of a connection of weight. As it can be seen from the equations [3], accumulation of information during the choice process is degenerated by parameters like the decay rate, inhibition, noise, etc.
Depending on the rate of disappearing information, choice process may correspond to incorrect responses. When the decay and inhibition parameters are equal to zero, the terms in equations describing leak and competition disappear.
During evolution of the LCA model, when decay is larger than inhibition, the threshold is reached when noise pushes the system away from the attractor. If the inhibition is larger than decay, the dynamics is characterized by repulsion from the fixed point. It is known as a primacy effect.
Once a accumulator in the LCA model hits the upper boundary, it terminates the decision process. When the activation reaches a given criterion, the participants make a preliminary decision (stop integrating input). The time courses of average responses from population of LIP neurons cease increasing. The effect of early input may lead to premature choice.
We can see from the behavioral research in decision making that humans and animals violate expected-value prescriptions and change their preferences depending on the way the options are described and on a contextual factors.
Stochastic switch of attention across dimensions
Humans and animals prefer the less risky of two options [20]. Risk-aversion or risk-seeking depends on a reference, information on an expected state, which is subject to manipulation. The question is how to explain preference reversals? [21].
The Bernoulli diminishing return intuition says that there are neural representations transforming their input (objective value) under a logarithmic type of nonlinearity. (A logarithmic function u(x) = log10(x) is used as the expected utility). Paying a large amount of money results in a high probability of making a loss and a small probability for a high win [3]. The output is subject to additional independent noise of constant variance c2. It can result to reversal effects with higher slope for losses than for gains. The variance in the neuronal firing rate of neurons is approximately proportional to the mean firing rate. It was proposed a typical relationship between the mean and the variance of the inputs as 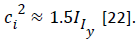 A logarithmic utility function relates to the need to combine utilities across dimensions. To maximize this utility function, we must maximize a combination of linear and multiplicative terms. For two dimensions:
A logarithmic utility function relates to the need to combine utilities across dimensions. To maximize this utility function, we must maximize a combination of linear and multiplicative terms. For two dimensions: 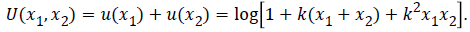 Multiplicative term in the utility optimization is supported by a survival rationale (rather joined than separate).
Multiplicative term in the utility optimization is supported by a survival rationale (rather joined than separate).
There is a logarithmic dependency on gains and losses. The utility evaluation has also reference dependence. The reference depends on the subjective expectations and on the accessible information of decision maker [23]. The preference compromise (0.5,0.5) has a much better utility than the (1,0) option. Nonlinearities in the value function can explain riskaversion and preference reversal in choice between alternatives characterized across multiple dimensions. The need to trade arises between the utility with different objective values among options associated with a given monetary values not only in risky choice but also in a case of multidimensional choice.
Discussion
Because neural activities are noisy, competition between distinct peaks of activity cannot follow only a simple ‘winnertake- all’ rule, or random fluctuations would determine the winner each time, rendering informed decision making impossible.
Excitation in colour cue pushes the group of neurons of PFC towards stronger activity than other. This causes unbalanced competition in the dorsal premotor cortex (PMd) and one peak increases its activity. Why we deducing that the other must be at same time automatically suppressed? On the other hand, differences at the activity levels may be seen as equivalent to a decision and the GO signal may be given [2].
We could not agree with views, that small differences in the levels of activity should be ignored by the system. In Prigogine’s ‘far-from-equilibrium’ dynamics, small differences may lead to new phenomenon in the system [24]. From the same reasons we argue, that suppressions of its opponents can be allowed everywhere, it may lead to higher entropy of transfer probabilities and hence to a deceptive results.
There should be a threshold (s) of activity, above which a particular peak (s) limits of the final response choice. Decisions are made when neural activity reaches some thresholds emerging from the nonlinear dynamics between competing populations of neurons.
It was shown in the interrogation paradigm that a balance of decay and inhibition does not optimize error rate (ER) for the bounded LCA model [3].
For view presented in this paper is of central importance to note, that the switch like reversal, repulsion in selection of actions could be caused not only by trade in unit probabilities (stochastic rules), but also by switch in biological motor control (biological constraints).
The biggest limiting factor in recent decision-making research in neuroscience are applications using also elements of the reductionist strategy. Partly, there was this risk concerning the most ambitious quantitative projects like Edelman’s NSI ‘Darwin’ series, H. Markram’s IBM Blue Brain, Sejnowski’s ‘Neural Computation’ school, or Penrose’s school, etc., that they can try to implement platonic mathematical fundamentalist ideas in computation of choice processes.
Let me allowed to cite the presentation of the results of the IBM Blue Brain project at the European Future Technologies meeting in Prague. Not all of interested have agreed that the ultimate goals of the Blue Brain project were achievable. Wahlster of the German Research Center for Artificial Intelligence, and a chief German government scientific adviser on ICT told that the reductionist strategy of the project has flawed-that it won’t see the forest for the trees. This is very interesting research…but doesn’t help us in computer science in having the intelligent behavior of humans replicated [25].
H. Markram, leader of the Blue Brain project have also argued “in contrast to Turing machines, generic computations by neural circuits are not digital, and are not carried out on static inputs, but rather on functions of time” [26]. It is still a question that by building up from one neocortical column to the entire neocortex, the ethereal emergent properties characterizing human thought will, step by step make themselves apparent. Things of higher brain functions cannot be easily predicted by just knowing and putting together elements and explore the principles, where they came from. This may be appropriate only for recognition automata, like is Edelman’s ‘Darwin’ [27]. Which are those “emergent properties” leading to “the very essence of being human”, and as such characterize human thought? Basically that’s what we are after: understanding the principles of emergent properties said Markram and aided that…it was simply a matter of money [25]. I am afraid, that these very optimistic declarations are… about money.
Given that higher brain functions are a rich biological and psychological phenomenon, a satisfactory neural theory about these questions must avoid reductionistic excess. Any theory that identifies psychology with a single measure is likely to be excessively reductionistic and, as a result, limited in its scope. The development and simultaneous application of multiple quantitative measures would more appropriately characterize the relevant complexity of the neural systems underlying higher psychic functions. We can just agree that some aspects of these functions are likely to resist quantification altogether. An adequate theory is therefore likely to be one that consists of a combination of qualitative and quantitative elements [28]. What is missing from above account is a sober scientific analysis related to thoughts process: an account of real psychology, of real brains and conversion of their underlying biology. Human mind can solve the ‘Entscheidungs problem’, therefore as ‘super-mind’ is not only a recognition automata, because capable of processing information not Turingcomputable.
Knowing the state of every neuron and every synapse in a model, one can analyze the mechanisms involved in neural computations with a view toward development of novel computational paradigms based on how the brain works [29].
Probably it will need a new definition of non-Shannon not- Turing computable functions [30,31]. Above biological constraints contribute to losses during decision making in a terms of informational entropy and have a common denominator: not adequate theory of biological information allowing for emergence of real psychology reflecting a needed complexity and neurothermodynamical depth of higher brain functions specifics.
9553
References
- Gold JI, Shadlen MN (2007) The Neural Basis of Decision Making. Annual Review of Neuroscience 30: 535-575.
- Cisek P (2007) Cortical mechanisms of action selection: the affordance competition hypothesis. Philos Trans R Soc Lond B Biol Sci 362: 1585-1599.
- Bogacz R, Usher M, Zhang J, McClelland (2007) Extending a biologically inspired model of choice: multialternatives, nonlinearity and value-base multidimensional choice. Philosophical Transactions of the Royal Society B.
- Bogacz R, Gurney K (2006) The basal ganglia and cortex implement optimal decision making between alternative actions. Neural Computation 19: 442-477.
- Isoda M, Hikosaka O (2008) Role for Subthalamic Nucleus Neurons in Switching from Automatic to Controlled Eye Movement. The Journal of Neuroscience 28: 7209-7218.
- Roxin A, Ledberg A (2008) Neurobiological Models of Two-Choice Decision Making Can Be Reduced to a One-Dimensional Nonlinear Diffusion Equation. PloS Computational Biology 4.
- Kornblum S, Hasbroueq T, Osman A (1990) Dimensional overlap: cognitive basis for stimulus-response compactibility-a model and taxonomy. Psychol Rev 97: 253-270.
- Fusi S, Assaad W, Miller EK, Wang XJ (2007) A neural circuit model of flexible sensorimotor mapping: learning and forgetting on multiple timescales. Neuron 54:319-333.
- Eigen M (2002) Error catastrophe and antiviral strategy. PNAS 99: 13374-13376.
- Eigen M, Ohta T (1971) Population Genetics. Princeton Univ Press, Princeton, NJ.
- Hamming RW (1980) Coding and Information Theory. Prentice-Hall, EnglewoodCliffs, NJ.
- Chevalier G, Vacher S, Deniau JM, Desban M (1985) Disinhibitions as a basic process in the expression of striatal functions. I. The striato-nigral influence on tecto-spinal/tecto-diecenphalic neurons. Brain Res 334: 215-226.
- Anderson SW, Bechara A, Damasio H, Trantei D, Damasio AR (1999) Impairment of social and moral behavior related to early damage in human prefrontal cortex. Nature Neuroscience 2: 1032-1037.
- American Psychiatric Association(1994) Diagnostic and Statistical Manual of Mental Disorders. Fourth Edition. Washington, DC: American Psychiatric Association.
- Raine A, Lencz T, Bihrle S, LaCasse L, Colletti P (2000) Reduced Prefrontal GrayMatter Volume and Reduced Autonomic Activity in Antisocial Personality Disorder. The Archives of General Psychiatry 57: 119-127.
- Haare RD (1991) Manual for the Hare Psychopathy Checklist-Revised. Multi Health Systems, Toronto.
- Honey CJ, Kotter R, Breakspear M, Sporns O (2007) Network structure of cerebral cortex shapes functional connectivity on multiple time scales. PNAS104: 10240-10245.
- Kelsey HT (2005) Quantum Darwinism. The reality of reality ? Los Alamos National Laboratory Newsletter 6: 1-4.
- Kahneman D, Tversky A (Eds.) (2000) Choices, Values and Frames. Cambridge University Press.
- Tversky A, Kahneman D (1979) Prospect Theory: An Analysis of Decision under Risk. Econometrica 47: 263-292.
- Shadlen MN, Newsome WT (1998) The variable discharge of cortical neurons:implications for connectivity, computation, and information coding. Journal ofNeuroscience 18: 3870-3896.
- Kahneman D (2003) Maps of Bounded Rationality: Psychology for BehavioralEconomics. The American Economic Review 93: 1449-1475.
- Prigogine I (1997) The End of Certainty. Time, Chaos, and the New Laws of Nature. Free Press, New York.
- Palmer J (2009) Simulated brain closer to thought. BBC News. https://news.bbc.co.uk/go/pr/fr/-/2/hi/science/nature/8012496.stm
- Maass W, Natschlager T, Markram H (2002) Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Computation14: 2531-2560.
- Reeke GN, Sporns O, Edelman GM (1990) Synthetic neural modeling: the ‘Darwin’ series of recognition automata. Proc IEEE 78: 1498-1530.
- Seth AK, Izhikevich E, Reeke GN, Edelman GM (2006) Theories and measures of consciousness: An extended framework. PNAS 103: 10799-10804.
- Izhikevich EM, Edelman GM (2008) Large-scale model of mammalianthalamocortical systems. PNAS105: 3593-3598.
- Shannon CE (1948) The Mathematical Theory of Communication. Bell SystemTechnical Journal 27: 379-423.
- Tribus M, McIrvine EC (1971) Energy and Information. Scientific American179-184.




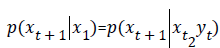
 then the assumption of a Markov process is invalid. Incorrectness of assumption expressed by the TE, as the Kullback-Liebler entropy:
then the assumption of a Markov process is invalid. Incorrectness of assumption expressed by the TE, as the Kullback-Liebler entropy: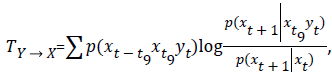
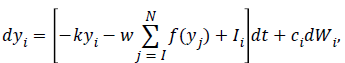
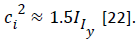 A logarithmic utility function relates to the need to combine utilities across dimensions. To maximize this utility function, we must maximize a combination of linear and multiplicative terms. For two dimensions:
A logarithmic utility function relates to the need to combine utilities across dimensions. To maximize this utility function, we must maximize a combination of linear and multiplicative terms. For two dimensions: 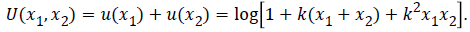 Multiplicative term in the utility optimization is supported by a survival rationale (rather joined than separate).
Multiplicative term in the utility optimization is supported by a survival rationale (rather joined than separate).