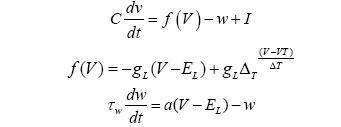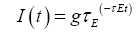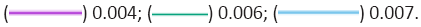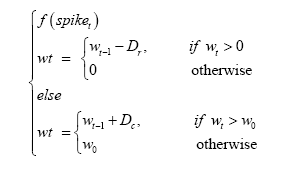Review Article - (2023) Volume 0, Issue 0
Received: 21-Jun-2023, Manuscript No. IPJNN-23-13850; Editor assigned: 23-Jun-2023, Pre QC No. IPJNN-23-13850(PQ); Reviewed: 07-Jul-2023, QC No. IPJNN-23-13850; Revised: 14-Jul-2023, Manuscript No. IPJNN-23-13850(R); Published: 21-Jul-2023, DOI: 10.4172/2171-6625.14.S7.003
Cell Assemblies (CAs) are the neural basis of both long and short term memories. CAs, whose neurons persistently fire, are active short term memories while the neurons are firing, and the memory ceases to be active when the neurons stop firing. This paper provides simulations of excitatory spiking neurons with small world topologies that persist for several hundred milliseconds. Extending this model to include short term depression allows the CA to persist for several seconds, a reasonable psychological duration. These CAs are combined in a simple associative memory so that when three CAs are associated, ignition of two causes the third to ignite, while pairs of unassociated CAs do not lead to the ignition of other CAs. This mechanism has a larger capacity than a Hopfield net. A discussion of the current psychological theories, other mechanisms for short term memory, the strengths and weaknesses of the paper’s simulated models, and proposed challenges are also provided.
Cell assembly; Spiking neuron; Short term memory; Associative memory; Short term depression
Cell assembly; Spiking neuron; Short term memory; Associative memory; Short term depression
A long standing hypothesis is that Cell Assemblies (CAs) are the neural basis of many psychological phenomenons such as concepts [1]. So, the neural basis of the concept dog is a CA, a set of neurons with high mutual synaptic strength. When the concept is present in short term memory, the neurons are firing at an elevated rate; so the CA is the basis of both long and short term memory. While this long standing hypothesis has many adherents, and is frequently used in the simulation literature, little work exists using persistently firing CAs as the basis of short term memory [2-5].
While it is relatively easy to simulate CAs that persist indefinitely, it is more difficult to get them to persist for seconds, and then autonomously cease firing, like psychological short term memories [6,7]. Section 3 shows a series of simulations using small world topologies of spiking point neurons that persist once ignited, and then spontaneously cease firing. These simulations use point models that are widely used in neurobiological simulations. Section 4 shows an extension of the small world model using short term depression, which supports flexible firing duration, and thus flexible short term memory on the order of seconds.
One of the problems with indefinitely firing CAs is that they are typically not calculating anything, but simply keeping a short term memory active. For CAs to be effective, they need to calculate something. It is theorized that CAs perform many tasks beyond holding items in memory including spatial localization and mapping, acting as the semantic pole of symbols such as words, and associative memory [8-11]. As the neural basis of symbols, they act as active symbols [12]. Section 5 describes simulations of associative memory, with triples of associated CAs. These have an increased capacity over Hopfield nets, with two CAs retrieving the third associated CA. The paper concludes with a discussion that positions the model within the overall computational cognitive neuroscience context. The final section summarizes.
The neural basis of short term memory is poorly understood. Indeed the basics of psychological short term and working memory are under debate. The standard model of short term memory is that a CA of neurons fifires persistently to maintain the active short term memory.
Short term memory
Short term memory is an important aspect of cognition, including human cognition [13]. Short term memory and working memory are often conflated but they can be viewed as a continuum with working memory centred on attention and a small number of items in working memory. Short term memory may be larger and less central to processing [14-16]. See section 6.1 for further discussion of short term and working memory and current neuropsychological theories. The standard theory, deriving from is that cognitive items in short term memory have their neurons firing at an elevated rate [1]. The neurons associated with a cognitive item are the neural basis of that CA.
Cell assemblies
A CA is learned using Hebbian learning. Indeed, Hebb proposed the CA and Hebbian learning in tandem [1]. Neurons fire repeatedly in response to stimulus, and as these neurons fire, their mutual synaptic strength increases. Eventually, this strength is sufficient to sustain a reverberating circuit, a CA, and the CA can continue to fire without external stimulus. When a stimulus is presented with sufficient strength, the reverberating circuit is said to ignite. The cognitive unit the CA represents is in short term memory while spiking at an elevated rate. In the standard model, when the reverberating circuit ceases to fire, the cognitive unit has left short term memory.
There are long standing computational models of CAs [17,18]. Here the system represents a set of neurons that have particular parameters. When sufficient activity is sent into the system, the CA ignites, then follows a Snoopy curve of activation. That is the system initially has a burst of activity, then the activity gradually decreases, until it can no longer support the reverberating activity and then the activity, collapses to below the baseline activity. (It is called a Snoopy curve because a plot of neurons firing by time looks something like Snoopy lying on his dog house.) Unfortunately, these models have not been simulated in spiking neurons.
Binary cell assemblies
It is relatively easy to construct a topology of point neurons that, once ignited, persists indefinitely [6]. With Leaky Integrate and Fire (LIF) neurons, a small number of well-connected neurons is sufficient. If they all spike, they will activate each other causing them all to spike repeatedly. If the neurons have adaptation, two or more sets of neurons can activate each other like a synfire chain [19]. These are binary because they are either on or off. These are similar to spin glass models, and other well connected topologies. For example, the Hopfield net, once started, moves to a stable state that persists indefinitely [20]. While it is relatively easy to construct complex procedural logic with binary CAs, their behaviour as short term memory items is poor. Short term memory does not persist indefinitely.
Point models of neurons
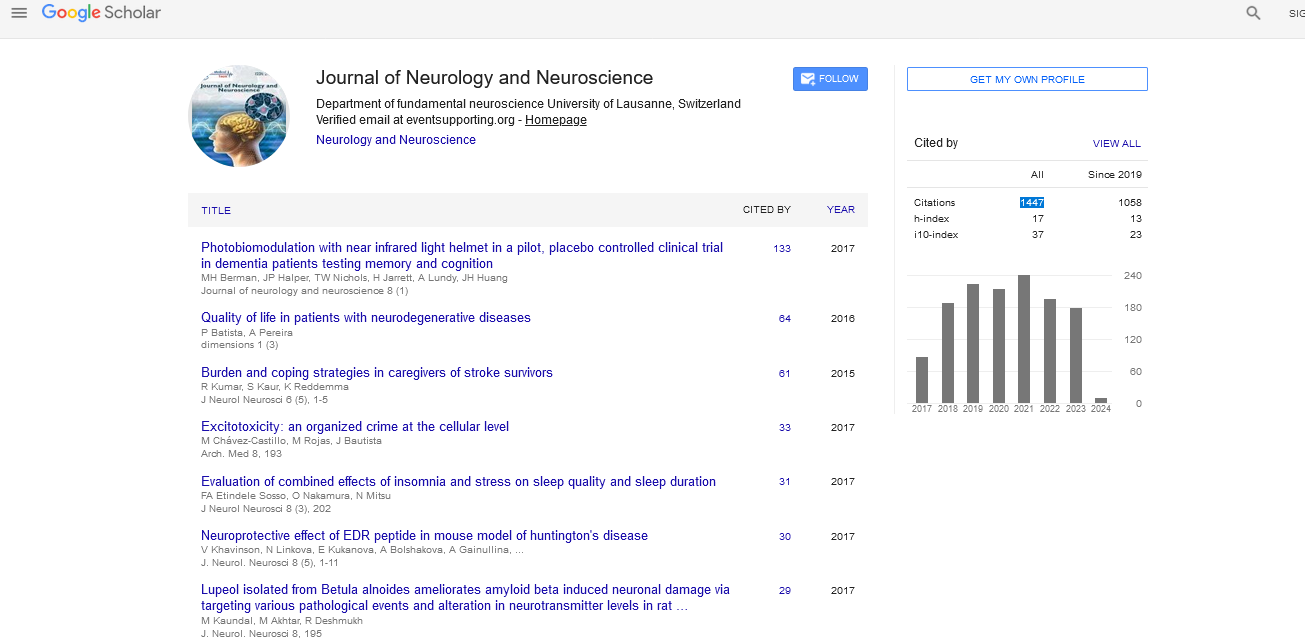
Point models are approximations of neurons based on relatively simple equations. More complex models exist but are computationally expensive to simulate [21]. These models vary in their fidelity, and typical parameter settings do not reflect the wide variety of biological neural behaviour, and indeed many models cannot approximate many types of bio- logical neurons such as bursty neurons. Moreover, models are often extended by synaptic models. There are many common point models including reverberate and fire models leaky integrate and fire models, and leaky integrate and fire models with adaptation for a review or for an analysis of several point models) [22-25]. The standard interpretation is that neurons have activation, and they collect the activation from other neurons, via synapses, when those neurons fire. That activation leaks away over time. The model used in the simulations below is a leaky integrates and fire models with adaptation [23]. It is implemented in PyNN and NEST [26,27]. The model is based on equations 1-3.
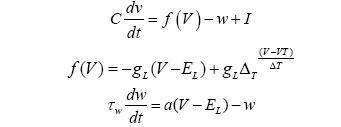
V is the variable that represents the voltage of the neuron, and t the variable for the time. C is the membrane capacitance constant, and I is the input current. w is an adaptation variable initially 0 and determined by equation 3; most neurons have adaptation making the firing rate decline under constant input [28]. gL is the leak conductance constant and EL is the resting potential constant. ∆T is the slope factor constant and VT is the spike threshold constant. τw is the adaptation time constant. Equations 1 and 2 determine the change in V (the voltage variable), and equation 3 manages the change in w (the adaptation variable). These variables are also changed when V>VT and the neuron spikes, V is reset to EL, and w is increased by a constant b for spike triggered adaptation. The simulations described below in this paper use the default constants described by Brette and Gerstner [23]. The synapses transmit current over time at an exponentially decaying rate described by equation 4 [29].
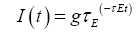
g is the strength of the synapse, and τE is the speed constant. Again, the default constant (from PyNN) is used in the simulations below.
There are a wide range of biological neuron types, but regularly spiking pyramidal neurons are common in the cortex [30]. This spike without input, which is called spontaneous firing [31]. These are the type of neurons that are being modelled in this paper. While it is possible to change the parameters of the leaky integrate and fire model with adaptation to cause it to fire spontaneously, this leads to spontaneous CA reignition after initial ignition; a set of spike sources has instead been used (as is commonly done) [32]. Consequently, when unstimulated, the neurons fire spontaneously. This can be seen in Figure 1, which shows a set of 1000 neurons over 4000 ms. There is no external input except for each neuron is forced to fire 5 times at 1000 ms. The plot shows initial spontaneous firing, followed by the external activation based firing at 1000 ms., a period of no firing due to adaptation, and then a return to spontaneous firing.
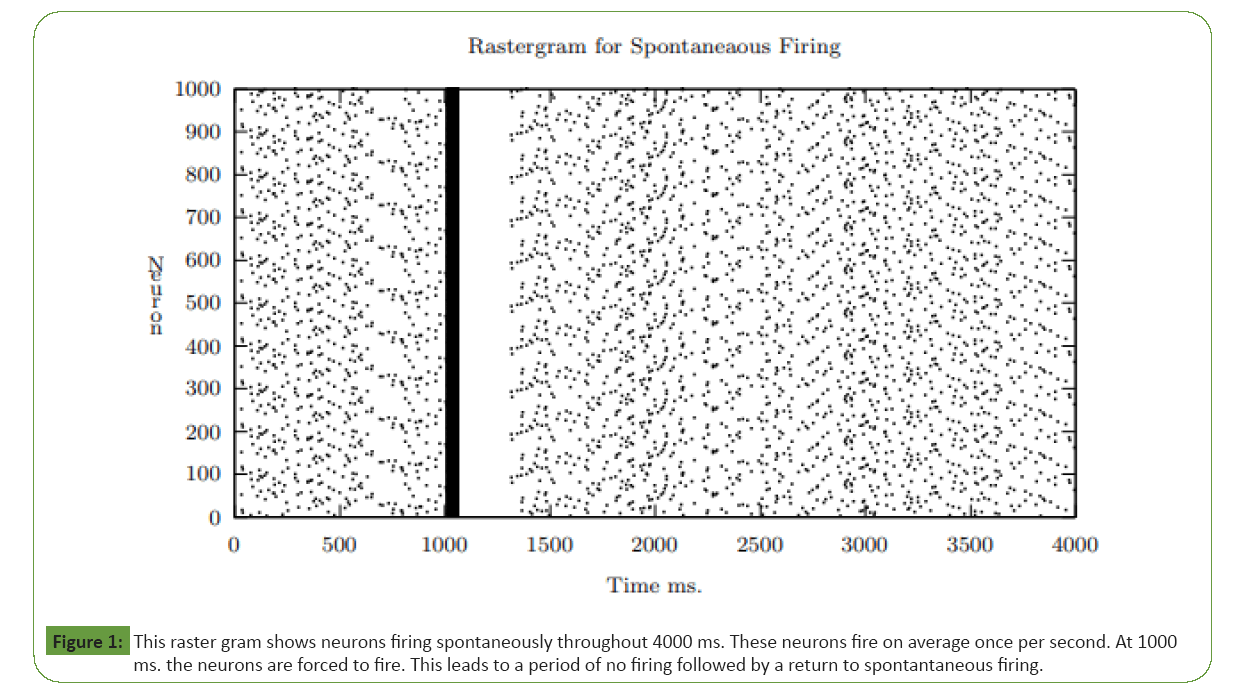
Figure 1: This raster gram shows neurons firing spontaneously throughout 4000 ms. These neurons fire on average once per second. At 1000 ms. the neurons are forced to fire. This leads to a period of no firing followed by a return to spontantaneous firing.
Small world topology
Small world topologies are widely used to make simulated neural topologies and are characterised by a rich get richer topology. For example, Bohland and Minai use a small world topology to analyse retrieval of autoassociative memories, which is quite similar to CA ignition though the units are binary nodes following [20,33]. Hopfield, Zemanov´a, Zhou use a network of network of networks to explore synchronous behaviour. Both individual networks and connections between nets are small world. Individual nets map to brain areas, and connections map, both functionally and by biological connectome data [34].
Psuedocode for small world topology creation
Allocate n-n synapses
Existing-synapse-count=n*number-neurons for each neuron for each new synapse
Pre-synaptic-neuron=neuron
Target-number=random (0, existing-synapse-count)
Target-neuron=neuron-of-synapse-number (target-number)
Post-synaptic-neuron=target-neuro
Creates synapse (pre-synaptic-neuron, post-synaptic-neuron)
Existing-synapse-count +=1
Simulations below use a small world topology. Neurons all have the same number of synapses leaving each neuron to other neurons in the CA. However, incoming synapses are allocated by the small world topology. This is done following the algorithm described in equation 1. Initial synapses are allocated so that each neuron has the same number of incoming and outgoing synapses (allocate n-n synapses). Typically, each has one leaving and one entering (n=1). Then new synaptic targets are allocated by a rich get richer scheme. The first post-synaptic target neuron is selected randomly, but the second is twice as likely to be allocated to that same target as to any other neuron. Repeating this leads to a zipf distribution of incoming synapses with many neurons having few incoming synapses, and some having many [35]. Concern about the length of synaptic paths in nets formed as random graphs is related to small world topologies. Small world topologies have short path lengths as an intrinsic property [36]. There is evidence that biological topologies are small world [37]. This lends some additional biological support for this model.
Persistence and energy
The energy of a neural system, particularly a simulated one, can be measured by its voltage, its spikes or a combination of these. When a neuron fires, its voltage is typically reset, but voltage is then spread to its post-synaptic neurons. A CA has a relatively low background energy, which increases rapidly when it ignites. The energy then drops when the circuit stops reverberating. Figure 2 shows the behaviour of a small world topology with a moderate level of input (see supplementary section for details). Figures 2-4A show the number of neurons, of the 1000 in the CA, firing per 1 ms. time step. The same coarse topology is used for all three runs, but the synaptic weight is varied. Spontaneous firing can be seen by all three before initial external activation is provided at 150 ms. The lower synaptic weight CA fails to ignite with 50 neurons fired, and spontaneous firing continues; the initial spikes do not produce enough energy to cause ignition. The middle weighted CA ignites, and persists for approximately 600 ms and then spontaneous firing returns. The initial spikes cause an increase in energy sufficient for ignition. Adaptation then allows the threshold to maintain reverberation to increase, and the CA stops reverberating. The largest weighted CA fires indefinitely; the plot shows firing for 4000 ms but runs to 100,000 ms (and perhaps indefinitely beyond) with the CA persistently firing throughout; in this case, adaptation is insufficient to stop reverberation. It is relatively easy to construct a network that fires indefinitely, but more difficult to make one that stops after seconds of firing.
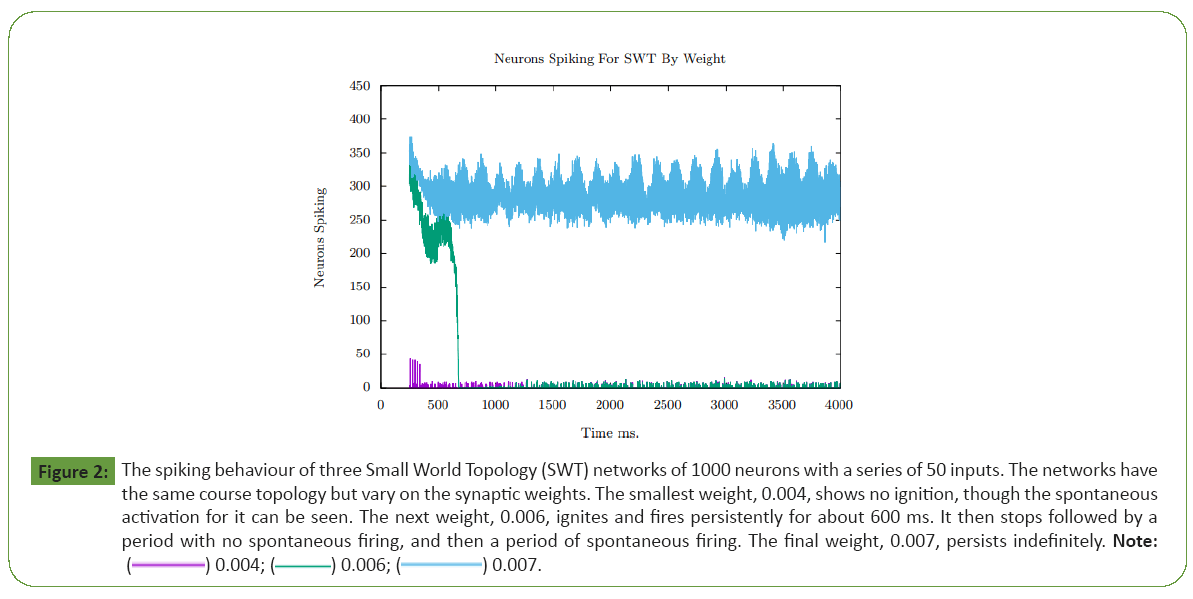
Figure 2: The spiking behaviour of three Small World Topology (SWT) networks of 1000 neurons with a series of 50 inputs. The networks have
the same course topology but vary on the synaptic weights. The smallest weight, 0.004, shows no ignition, though the spontaneous
activation for it can be seen. The next weight, 0.006, ignites and fires persistently for about 600 ms. It then stops followed by a
period with no spontaneous firing, and then a period of spontaneous firing. The final weight, 0.007, persists indefinitely. Note:
Figure 2 shows a group of neurons that does not ignite (0.004), a self-terminating short term memory (0.006), and a short term memory that persists indefinitely (0.007) unless shut off by some other process. As short term memory is supported by persistent firing, the underlying long term memory is formed by the topology, which is the synaptic connectivity and the weight. The author found no topologies with random synaptic connectivity that had self-terminating persistence.
The small world topology lowers the energy that is needed to ignite the CA. Since the distribution of incoming synapses is skewed so that some neurons have many more, it takes fewer initial neurons, on average to make those neurons fire. As those neurons fire, they increase the overall energy of the CA, and it ignites. Similarly, when those neurons have increased adaptation leading to lower firing rates, they can cause a loss of activity that stops the CA’s reverberation. That is, with less synaptic strength, there is insufficient energy to ignite the CA. With moderate synaptic strength, enough energy is generated for the CA to ignite; moreover, as adaptation increases, the energy is no longer sufficient to support reverberation, and the neurons in the CA stop firing. With even more synaptic strength, the CA ignites, but energy generated overcomes adaptation and the CA persists indefinitely.
Extending persistence via short term depression
While persistence for several hundred ms. is useful, the standard theory states that while the short term memory is active, the neurons in the CA are firing at an elevated rate. As it is clear that short term memories can persist for at least several seconds, a spiking CA model that persists for several seconds is needed.The model from section 3 is made up entirely of excitatory neurons with adaptation and synapses whose weights do not change (static synapses). See section 6.2 for neural systems without inhibition. This section uses a modified synaptic model that has Short Term Depression (STD) [38,39] Figure 2. The short term depression is linear. When the neuron spikes, its post-synaptic synapses decrease in weight down toward 0, and when it does not spike, the weight increases back toward its original weight (equation 5)
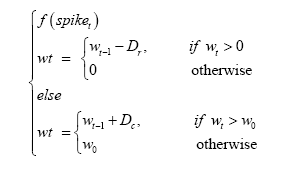
wt is the weight of the synapse at time t and w0 is the initial weight. wt-1 is the weight from the prior step. Dr and Dc are the synaptic weight change (reduction and increase) constants.
A simple extension of the system from Figure 2 yields a CA that persists for roughly 4000 ms, a psychologically realistic time. This is shown in Figure 3 the modification is that each synapse is split into a static and an STD component. The initial overall weight is similar to the 0.007 weight, but over the 4000 ms. the weight of many of the synapses decreases leading the CA to cease reverberating, (See the supplementary material section for further details) ( Figure 3).
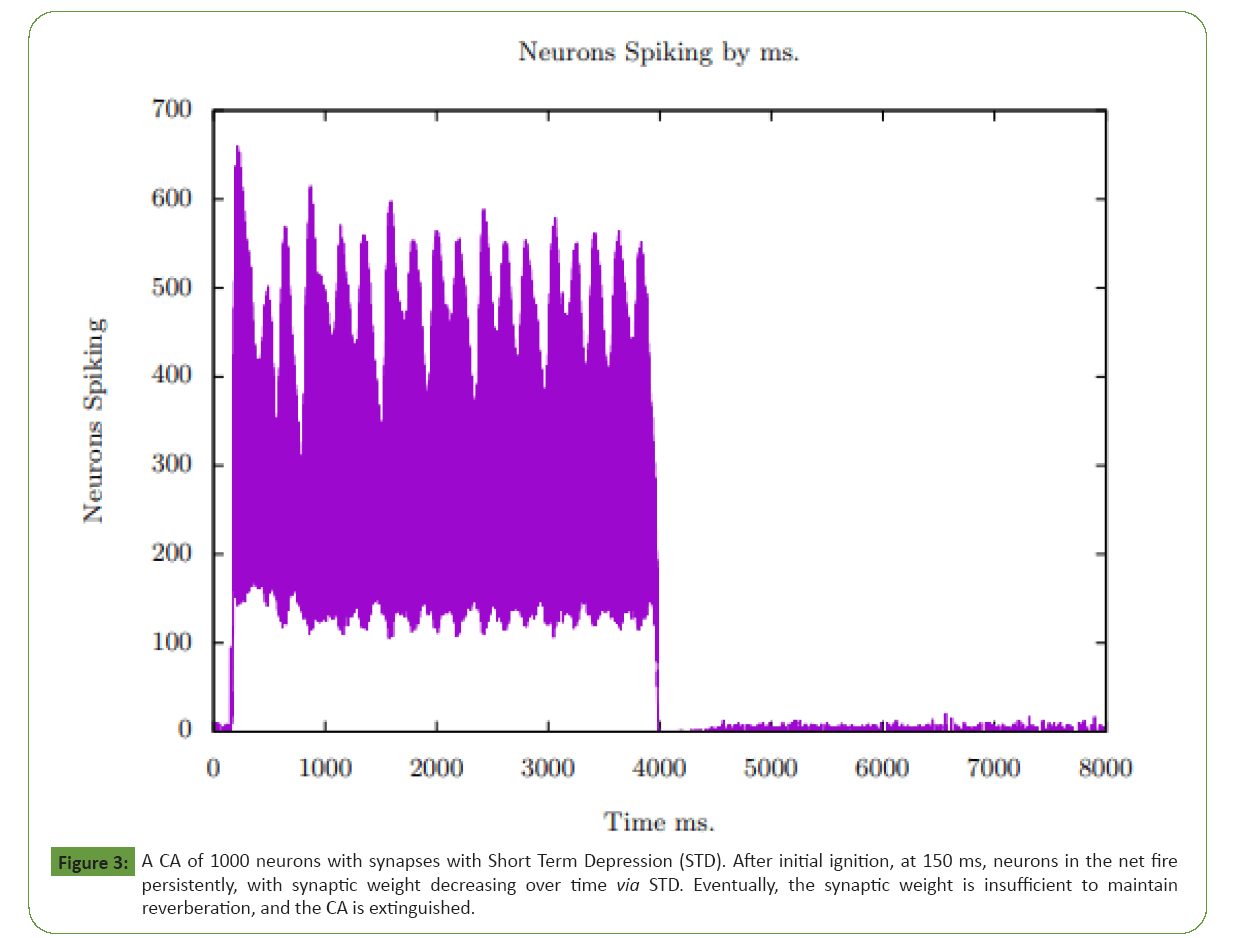
Figure 3: A CA of 1000 neurons with synapses with Short Term Depression (STD). After initial ignition, at 150 ms, neurons in the net fire persistently, with synaptic weight decreasing over time via STD. Eventually, the synaptic weight is insufficient to maintain reverberation, and the CA is extinguished.
CAs and associative memory
The CAs currently being simulated in the community are at best a metaphor of biological CAs. An extra constraint is that the CAs actually do some sort of calculation. As one of the main human cognitive components is associative memory, these simulations use a simple form of association. This is a three way association between primitive CAs. If two are presented, the third is retrieved. This type of association can account for psychological data [40]. An associative memory using five CAs is created. For the purposes of this paper, the CAs are labelled A0, B0, B1, C0, and C1, and there are two sets of three-tuple associations A0 − B0 − C0 and A0 −B1 −C1. The idea is that each of the CAs can be ignited and persist independently, as can the three way associations. Moreover igniting any pair of an association will lead to the full three-tuple igniting; a pair will retrieve its associated third. Finally, it is also important that unassociated pairs do not ignite any spurious CAs. So, for instance, igniting B0 and C1 enables them to fire persistently, but no third CA will ignite. If one is engineering a neural system to do this task, it is relatively straight forward. A simple translation from linear algebra would work similarly, a precise temporally decaying topology combined with a neural finite state automata would also work. However, it is entirely unclear how these topologies could be learned in a biological brain [41-44].
Figure 4A shows the number of neurons spiking per ms. in each individual base CA. Neurons in B0 are presented at 150 ms. leading to its ignition, and neurons in C0 are presented at 170 ms. leading to its ignition. As the two are associated they have elevated firing. The synaptic connectivity from both to A0, and the elevated firing rates of their neurons, is sufficient to ignite A0. B0 and C0 retrieve A0 in Figures 4A- 4D.
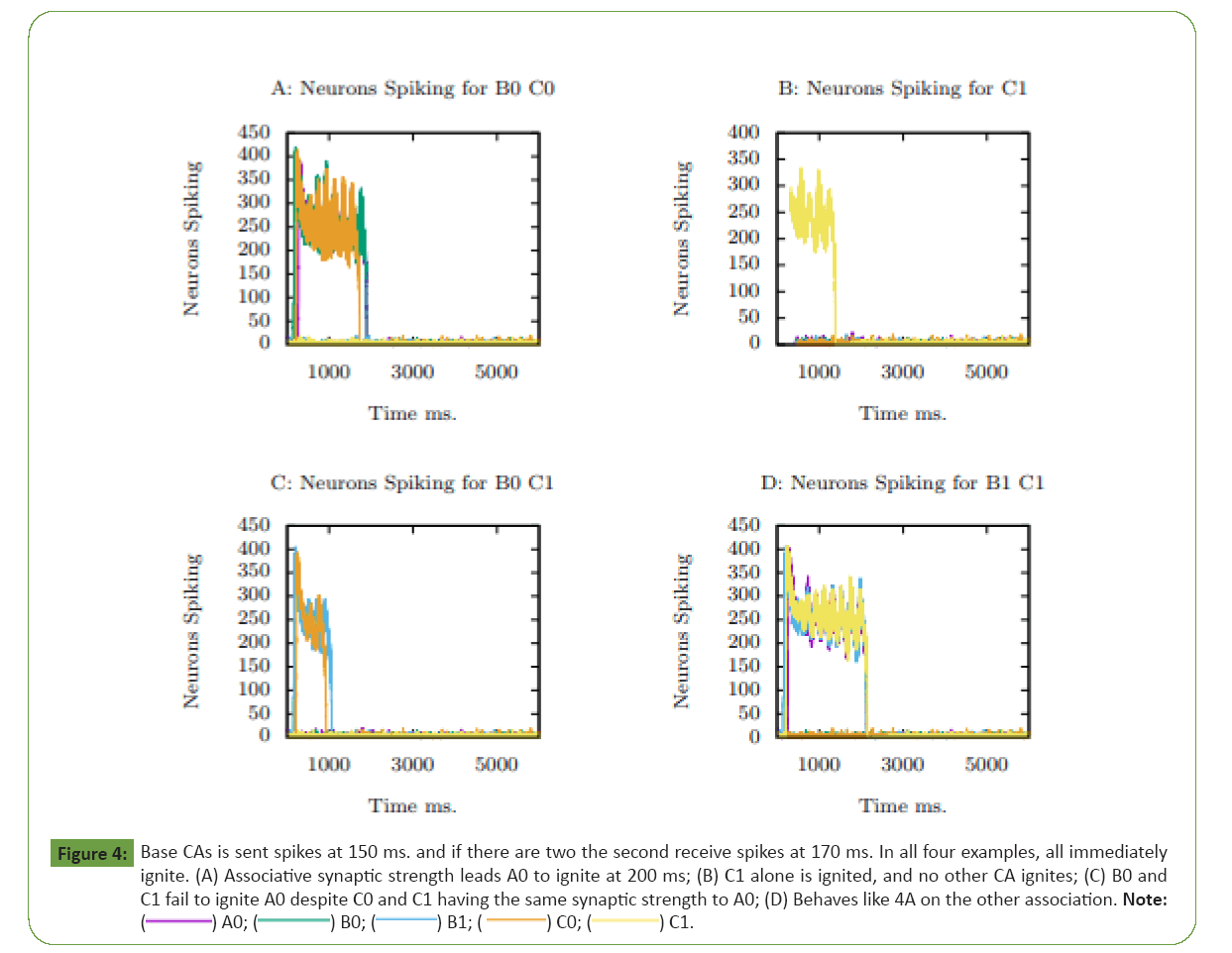
Figure 4: Base CAs is sent spikes at 150 ms. and if there are two the second receive spikes at 170 ms. In all four examples, all immediately
ignite. (A) Associative synaptic strength leads A0 to ignite at 200 ms; (B) C1 alone is ignited, and no other CA ignites; (C) B0 and
C1 fail to ignite A0 despite C0 and C1 having the same synaptic strength to A0; (D) Behaves like 4A on the other association. Note:
In Figure 4B, C0 is presented at 150 ms. and persists. This is an example of a single CA igniting and persisting.
In Figure 4C, B0 is present at 150 and C1 is presented at 170 ms. leading to their ignition. However, as the two are not associated, they do not fire at a faster rate. So, the two are insufficient to ignite A0 despite both C0 and C1 having the same synaptic weight to A0.
In Figure 4D, B0 is presented at 150 ms. and C1 is presented at 170 ms. leading to their ignition. Like Figure 4A, this also retrieves A0.
The CAs is each instances of the STD CAs from section 4. They are associated by randomly selected neurons from each pair with a small weight. Each neuron in CA has several low weighted synapses to the associated CA. The post-synaptic target neurons are randomly selected from the neurons in the target CA. A0 gets as much synaptic weight from the pair B0-C0 as from B0-C1. The reason that A0 is ignited by B0-C0 but not B0-C1 is that B0 and C0 fire at an elevated rate because they are associated. The synaptic strength that supports the association provides sufficient energy to A0 to ignite it, while the rate of the unassociated CAs is insufficient.
Note that synchrony plays a part in retrieval. When two associated CAs fire, they move into synchrony, as they stimulate each other. So, the incoming strength to the retrieved CA is greater. In the unassociated CAs, they continue to fire out of phase. This means that associative networks of CAs have a larger capacity than associative networks of Hopfield networks [20]. Hopfield nets of N nodes can only have N stable states. This simulation describes a network of five CAs, with seven stable states (the five individual CA states e.g. B1; the two associated states A0 −B0 −C0 and A0 −B1 −C1. If the four unassociated states B0 B1, B0 C1, B1 C0, and C0 C1 are considered, there are eleven states.). This of course is still on the order of N stable states. It does not require all CAs to be connected. For instance, B0 and C1 are not connected. However, all of the CAs in a triple need to be connected, and the triples can only share one CA. So, adding two new CAs, B2 and C2, enables a new triple A0 B2 C2 or B0 B2 C2 but not both. Adding two new CAs would also add new unassociated stable states; for A0 B2 C2, B0 B2 and others would be added. Negatively, the use of 1000 neurons per CA, which are each more computationally complex than a Hopfield unit, does not lead to a capacity win at least until there are a large number of CAs, and then it will be in unassociated CAs.
These states are also not stable, but pseudo-stable. They do stop, which allows new calculations. It is important that the CA network is actually doing a calculation during its processing and indeed a cognitive process [8]. Given two associated items, activate a third associated item. An example of what can be associated comes from [40]. If the CAs represent concepts like, B0 is has C0 is feathers, B1 is is, C1 canary, and A0 is bird. Presenting has and feathers retrieve bird. Presenting canary and is also retrieves bird.
It is hoped that simulation of neurons and neural systems will lead to better neurocognitive models and eventually an understanding of how the brain works to produce intelligent behaviour. However, the state of the art is quite some distance from anything like a complete understanding of how the brain produces intelligent behaviour; there is not agreement on the fundamental neural mechanisms that support psychological short term memory; and work in simulation is muddled by extensive use of biologically implausible models, and the difficulty of simulating a brain.
Working memory and short term memory
The evidence for the neural basis for working and short term memory is growing but is far from complete. It is clear that short term memories need to be represented neurally by a mechanism that largely reverts to the original state of the overall system after the memory has stopped [45]. It is likely that there is not just one type of short term memory mechanism, but several. Working memory tasks, such as memorising digits, are quite different from tasks such as scene scanning and reading. Perhaps there is some difference between the fast and slow systems of the brain; working memory is involved in the slow system and its capacity is quite limited, where the slow system may use a different mechanism, which has a larger capacity. It is likely that, at least initially, a CA needs to ignite to be accessible as a short term memory in Figure 4A [46].
In the standard model, the long term memory is represented by a CA; when it is ignited, neurons in the CA fire at an elevated rate, and the CA’s cognitive unit goes into short term memory. After the memory has ceased, and transient effects, such as short term depression and potentiation and adaptation, have disappeared, the system reverts largely to its initial state. The system may have had some modification of the long term state by, for instance, long term depression and potentiation, but this aside, the short term memory leaves no residual effects. Several CAs can be dynamically composed to provide cognitive behaviour, and this can significantly reduce the dimensionality of the system, which in turn can simplify the analysis of brain and cognitive states [47]. While the standard model has substantial biological support, other mechanisms have been proposed more recently [48]. These include short term synaptic facilitation and excitatory inhibitory balance [11,49,50].
Work on simulated spiking nets with an excitatory inhibitory balance supports the development of powerful engineering applications of spiking nets [49]. The work is inspired by evidence that neurons in vivo have irregular Poison-like spiking statistics. When neurons are near their firing threshold, a small input can cause them to fire. In simulation, systems keep neurons near their firing threshold by a topology that balances excitatory and inhibitory input and makes use of fast synaptic current transfer. A formal mechanism for the calculation of a synaptic weight matrix that supports the changing value of dynamic variables, represented by the neural outputs, can create neural systems that have sophisticated behaviour, such as robot arm controllers. It is however unclear whether these systems actually represent biological neural.
A more promising modification to the standard model is the addition of Short Term Potentiation (STP). Here a CA ignites, but then terminates. However, STP makes it easier to reactivate the CA for some time. When an area of the brain is broadly activated, the recently activated CA, now supported by STP, is the CA that ignites (or in this case re-ignites). Evidence of such behaviour is shown in working memory tasks [13]. There is a proposed neural architecture for working memory involving STP and neurons that do not persistently fire [51].
Perhaps there is a continuum from short term (and working) memory items based on STP to those based on persistent firing. Of course, those based on STP still need the neurons to fire persistently to start the process.
Simulating and emulating biological networks
It is difficult to simulate or emulate a large number of neurons in real time as a system that is parallel to an animal. No system currently parallels a mammal, though there are more complete models of simple brains such as the nematode C. elegans [52]. Work with high performance computers still falls short of simulating billions of spiking neurons in real time. Some work has been done in simulating small sections of the cortex but in this case, only 217,000 neurons and not in real time. However the biological fidelity of these simulations shows the distance from biological reality of almost all current neural simulation work (including the simulations in this paper). Markram use 55 types of neurons, reflecting presence in particular cortical layers, biological synaptic connectivity, with short term plasticity, compartmental models, and other features [53].
Neuromorphic hardware can support larger networks of point neurons with, for example, SpiNNaker simulating roughly a billion spiking neurons in real time [54]. Perhaps more importantly, it is not entirely clear what to do with these neurons. Mere computational power is not the chief difficulty; it is understanding how large nets perform to elicit cognition. A rat has about a billion neurons, but how to go from spiking neurons to rat functionality is an open question [55]. Brains have developed in bodies and are driven by them and drive them. It is not entirely clear how to connect the body and the simulated or emulated brain, though there is work in spiking robots, and virtual agents [6,51]. Moreover, networks of simulated spiking neurons can be. Extremely powerful for example, balanced excitatory inhibitory networks can approximate complex robot control with less than 1000 spiking neurons and [49]. These balanced nets have several biologically implausible features, so are poor biological models, but may be important to the community’s understanding of larger brain nets. So, a model using spiking neurons does not mean the model is biologically accurate. The models of CAs above in this paper use only excitatory neurons. It is clear that some neurons are inhibitory, though it does seem likely that the inhibitory excitatory distinction is based on particular pairs of types of neurons [56,57]. However, it is not clear what the effective of inhibitory synapses is on the overall network. This paper has only explored excitatory synapse, and shows that without inhibition, the neurons can cease firing. Perhaps the effect of inhibition is to allow CAs to compete, to prevent simulated epilepsy, some other function, or a combination of these.
Plasticity and development
Perhaps the largest challenge to understanding brains is understanding plasticity. Beyond, but including this, is the basic challenge of understanding how the brain actually develops. While there has been extensive simulation work around simulating long term plasticity using spike timed dependent plasticity, and perhaps to a lesser extent other long term models, long term plasticity is far from understood [58,59]. Also, despite the use of a short term plasticity rule in some simulations above (section 4 and 5, and the recent work with its use in modelling short term memory (section 6.1), it is also far from understood. There is also an obvious interaction between short and long term memory. When short term potentiation supports firing, this can lead to further long term memory. That is, short term plasticity has a direct influence on long term plasticity. Moreover work in structural plasticity, growth and death of synapses and neurons, could be said to be in its infancy. It is very difficult to develop a system that parallels the developmental process [60]. A brain does not just pop into existence, but follows a long developmental process from the first neuron being formed in utero [61].This of course is based around structural plasticity. Work in developmental models has come from the cognitive architectures community. A purported common model for the basis of thought has arisen, along with long standing and successful work in cognitive architecture that makes useful AI systems and cognitive models [62]. While literature in this area links processes to neural behaviour the links are generally metaphorical.
Strengths and weaknesses of the model
The models presented in this paper have several strengths. One strength is that they are quite minimalist. While using spiking neurons, they are represented by simple point models (a leaky integrate and fire model with adaptation). Synapses are typically static, and in sections 4 and 5 the plasticity is only short term depression, and that model is simple. Perhaps most significantly, there are no inhibitory neurons. Despite this simplicity, the CAs represented by the models persist for psychologically plausible times, and complete the important task of associative memory retrieval. The hope is that persistence and completion will still be supported by more sophisticated models, and that this simplicity will provide latitude to extend these models to more sophisticated tasks. A strength not mentioned above is synchrony. Biological brains often have synchronous neural firing, which is evidence for the neurons being associated [63]. The simulations here show synchronous behaviour as can be seen by the regular oscillations in Figures 2-4A.
Strength is that models are available for engineering neural systems. The standalone CAs can easily be integrated as components of larger systems, and in particular as a form of associative memory that persists for small finite times. Unfortunately the system also has weaknesses, and the author feels that pointing out these weaknesses can lead to the future development of better CA models. Firstly, neurons in the CAs are in one base CA. Biologically many, and perhaps all CAs, share neurons with other CAs [64]. It might be argued that the neurons are in only one base CA, but they are in many higher CA three tuples. Secondly, the neurons in the simulations fire at a very high firing rate. This is probably due to a lack of inhibition and the necessity of building up adaptive components (adaptation in section 3 and temporarily reduced synaptic strength in section 4) that lead the CA to stop firing. Thirdly, though understanding of memory activation and reactivation is far from complete, there is support for the idea that a memory that is activated with more strength remains in STM for longer. Moreover if a memory is reactivated, it will persist longer than from the initial activation The models presented above do not behave in this fashion [7,65,66]. Finally, note that in the above simulations, the CAs terminates on their own, and no CA is left ignited. It is entirely plausible that biologically CAs compete so do not need to self-terminate; instead the overall system forces the ignited CA to terminate.
The overall task of simulating cognitive brain activity at a neural level is currently far from accurate. This paper has provided an example with simple neural models and topologies of self-terminating short term memory cell assemblies. These models have used small world topologies and short term depression; the energy of the systems described their behaviour. These have also been used to implement an associative memory that is able to retrieve a third CA when two associated CAs are presented; all three leave short term memory shortly after retrieval. The overall system has a slight improvement on capacity over a Hopfield network, again described by the CAs’ energy. This associative memory task makes the system more than a simple short term neural memory model. The long term goal of this work in simulation is to develop artificial spiking neural network models that accurately represent animal neural behaviour and animal psychological behaviour. The authors are unaware of other spiking network models, even simple ones, that accurately represent the self-terminating persistently firing CAs spiking nets. As such, this paper provides a base line system, a straw man that can be used to explore neural psychological models of short term and associative memory.
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
[Crossref] [Google scholar] [PubMed]
Citation: Huyck CR (2023) A Spiking Model of Cell Assemblies: Short Term and Associative Memory. J Neurol Neurosci Vol. 14 No.S7:003
