Research Article - (2023) Volume 0, Issue 0
Golden Ratio Information for Neural Spike Code
Bo Deng*
Department of Mathematics, University of Nebraska-Lincoln, Lincoln, Nebraska, USA
*Correspondence:
Bo Deng, Department of Mathematics, University of Nebraska-Lincoln,
Lincoln, Nebraska,
USA,
Email:
Received: 20-Jun-2023, Manuscript No. IPJNN-23- 13848;
Editor assigned: 22-Jun-2023, Pre QC No. IPJNN-23- 13848(PQ);
Reviewed: 06-Jul-2023, QC No. IPJNN-23- 13848;
Revised: 13-Jul-2023, Manuscript No. IPJNN-23- 13848(R);
Published:
20-Jul-2023, DOI: 10.4172/2171-6625.14.S7.001
Abstract
Spike bursting is a ubiquitous feature of all neuronal systems. Assuming the spiking states form an alphabet for a communication system, what is the optimal information precessing rate? And what is the channel capacity? Here we demonstrate that the quaternary alphabet of spike number code gives the maximal processing rate, and that a binary source in Golden Ratio distribution gives rise to the channel capacity. A multi-time scaled neural circuit is shown to satisfy the hypotheses of this neural communication system.
Keywords
Neural spike code; Spike bursting; Neural communication system; Scaled neuron model
Introduction
Claude E. Shannon’s mathematical theory for communication laid a corner stone for the information age in the mid-20th century. In his model, there is an information source to produce messages in sequences of a source alphabet, an encoder/transmitter to translate the messages into signals in time-series of a channel alphabet, a channel to transmit the signals, and a receiver/decoder to convert the signals back to the original messages [1]. The mapping from the source alphabet to the channel alphabet is a source-to-channel encoding. Any communication system is characterized by two intrinsic performance parameters. One, its Mean Transmission Rate (MTR) (in bit per time) for all possible information sources, such as your Internet connection speed for all kinds of sources, both wanted and unwanted. Two, its Channel Capacity (CC) which a particular information source or a particular source-to-channel encoding scheme can take advantage to transmit at the fastest data rate.
One property that is ubiquitous to all neurons is their generation of electrical pulses across the cell membrane. The form can be in voltage or any type of ionic current. The form is not important to our discussion but only the state of excitation or quiescence. We further simplify our discussion by considering only those type of neurons or neuronal circuit models which are capable of spike bursts. A spike burst is a segment of time-series which both begins and ends with a quiescent phase but with a sequence of fast oscillations of equal amplitude and similar periods in between. In terms of dynamics, the quiescent phase or the refractory phase is slow, and the spiking phase is fast, typical of fast-slow, multi-timed neural models, c.f. [2-5]. The fast-slow distinction between the two phases and the spike number count allow us to transform the analogue wave form into a discrete information system as an obvious assumption, see also [6].
So, if we construct a communication system using one neuron as an encoder/transmitter and another as a receiver/decoder, then what would be the best MTR and CC? More aptly, in a network of neurons, any interneuron plays the role of transmission channel, the same questions arise. That is, how much information the neuron can process in a unit time when it is open for any information and when it is restricted to information of a particular type?
Materials and Methods
Measurements of communication system
Table 1 lists the definitions of essential parameters and variables for any information system [7]. Given a source whose messages are sequences of its source alphabet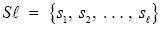 a source-to-channel encoding is a mapping from the source alphabet
a source-to-channel encoding is a mapping from the source alphabet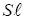 to the set of finite sequences of the system alphabet An so that a source sequence in
to the set of finite sequences of the system alphabet An so that a source sequence in 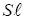 is translated to a sequence in An A particular source when source-to-channel coded in An is characterized by a probability distribution P, with Pk being the probability to find letter bk at any position of the encoded messages. According to the information theory, letter or base bk contains log2(1/Pk) bit of information for the encoded source, and a typical base on average contains H(p) bit of information for the encoded source. In statistical mechanics, the quantity entropy, H(p) is a measure of the disorder of a system, and in information theory, it is the measure of diversity for the encoded source. It is a simple and basic fact that the maximal entropy is reached if and only if the probability distribution is the equi probability,= 1/n,1≤k≤n and the maximal entropy is Hn=log2(n) From the designer’s point view of a communication system, the system is not for a particular source with a particular encoded distribution, but rather for all possible sources. For example, the Internet is not designed for a particular source but rather for all sources, such as texts, videos, talk-show radios, and so on. In other words, it is only reasonable to assume that each base bk will be used by some source, and it will be used equally likely when averaged over all sources. Hence, for any n-alphabet communication system, the maximal information entropy Hn=log2(n) in bit per base is a system-wise payoff measure for the alphabet.
is translated to a sequence in An A particular source when source-to-channel coded in An is characterized by a probability distribution P, with Pk being the probability to find letter bk at any position of the encoded messages. According to the information theory, letter or base bk contains log2(1/Pk) bit of information for the encoded source, and a typical base on average contains H(p) bit of information for the encoded source. In statistical mechanics, the quantity entropy, H(p) is a measure of the disorder of a system, and in information theory, it is the measure of diversity for the encoded source. It is a simple and basic fact that the maximal entropy is reached if and only if the probability distribution is the equi probability,= 1/n,1≤k≤n and the maximal entropy is Hn=log2(n) From the designer’s point view of a communication system, the system is not for a particular source with a particular encoded distribution, but rather for all possible sources. For example, the Internet is not designed for a particular source but rather for all sources, such as texts, videos, talk-show radios, and so on. In other words, it is only reasonable to assume that each base bk will be used by some source, and it will be used equally likely when averaged over all sources. Hence, for any n-alphabet communication system, the maximal information entropy Hn=log2(n) in bit per base is a system-wise payoff measure for the alphabet.
| Variableaverage ± SD |
Variableaverage ± SD |
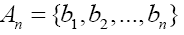 |
System alphabet for encoding, transmitting, and decoding. |
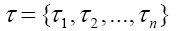 |
Base transmitting/processing time τk for base bk. |
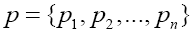 |
Probability distribution over An for an encoded source |
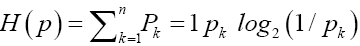 |
Averaged information entropy in bit per symbol of a particular source with encoded distribution p |
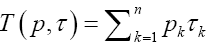 |
Averaged transmitting/processing time per symbol of a particular source with encoded distribution p. |
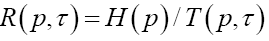 |
Particular transmission rate in bit per time of a particular source with encoded distribution p. |
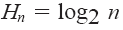 |
Maximal entropy Hn = maxp{H(p)} with the equiprobability, pk = 1/n, 1 ≤ k ≤ n, for all sources. |
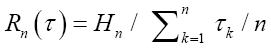 |
Mean Transmission Rate (MTR) in bit per time for all sources with the equiprobability. |
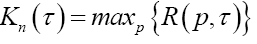 |
Channel Capacity (CC) with 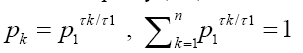 |
Table 1: Definitions for communication system parameters.
This does not mean that the larger the alphabet size the better the system. The balance lies in the consideration of the payoff against cost. The primary cost is the times the system takes to process the alphabet, such as to represent or to transmit the bases. Assume a base bk takes a fixed amount of time,τk to process. Then for the equi probability distribution, the average processing time is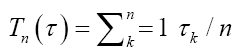 in time per base. Hence, the key performance parameter for an n-alphabet communication system is this payoff-to-cost ratio
in time per base. Hence, the key performance parameter for an n-alphabet communication system is this payoff-to-cost ratio 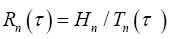 in bit per time, referred to as the Mean Transmission Rate (MTR) or the transmission rate for short. This is an intrinsic measure for all communication systems, regardless of the size nor the nature of their alphabets. As a result, different systems can be objectively compared. In the example of Internet, the transmission rate is the measure we use to compare different means of connection, such as coaxial cable, optic fiber or satellite. Notice also that the mean transmission rate is determined by all sources, and it is in this sense that the transmission rate is a passive measurement of a communication system.
in bit per time, referred to as the Mean Transmission Rate (MTR) or the transmission rate for short. This is an intrinsic measure for all communication systems, regardless of the size nor the nature of their alphabets. As a result, different systems can be objectively compared. In the example of Internet, the transmission rate is the measure we use to compare different means of connection, such as coaxial cable, optic fiber or satellite. Notice also that the mean transmission rate is determined by all sources, and it is in this sense that the transmission rate is a passive measurement of a communication system.
From the perspective of a particular source (user), its particular payoff-to-cost ratio is the source transmission rate, 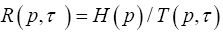 with p being its distribution over the system alphabet An This rate may be faster or slower than the mean rate Rn(p,τ). is no worse than the mean. The mathematical problem is to maximize the source transmission rate Rn(p,τ) over all choices of the distribution p. Solution to the optimization problem gives rise to the channel capacity (CC), denoted by Kn.
with p being its distribution over the system alphabet An This rate may be faster or slower than the mean rate Rn(p,τ). is no worse than the mean. The mathematical problem is to maximize the source transmission rate Rn(p,τ) over all choices of the distribution p. Solution to the optimization problem gives rise to the channel capacity (CC), denoted by Kn.
Result for neural spike code
The number of spikes in a burst for a neuron is called the spike number and without introducing extra notation we denote it by bk (as letters for the alphabet nA with the subscript k ≥ 1 for the spike number of the burst. The resultant alphabet system is referred to as the neural spike code.
We consider first the simplest case when the process time for the code progresses like the natural number: 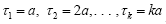 for code base
for code base 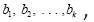 respectively, for a fixed parameter a. That is, the 1-spike base takes 1 unit of time in a to process; the 2-spike base takes 2 units of time in 2a to process and so on. Without loss of generality we can drop a by assuming a=1 for now.
respectively, for a fixed parameter a. That is, the 1-spike base takes 1 unit of time in a to process; the 2-spike base takes 2 units of time in 2a to process and so on. Without loss of generality we can drop a by assuming a=1 for now.
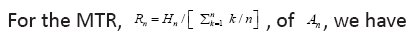
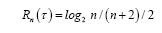
Since 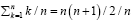 For
For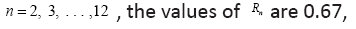 0.79, 0.80, 0.77, 0.74, 0.70, 0.67, 0.63, 0.60, 0.58, 0.55
0.79, 0.80, 0.77, 0.74, 0.70, 0.67, 0.63, 0.60, 0.58, 0.55
That is, the optimal spike code is A4 with the MTR R4 = 0.80, as one can easily show the function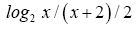 is a decreasing function for × > 4.
is a decreasing function for × > 4.
For the CC, Kn(τ) consider the binary spike case A2 first.
To simplify notation, we use 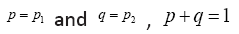 Then
Then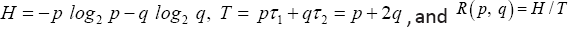 . We use the Lagrange multiplier method to the find the maximum R(p,q) of subject to the constraint
. We use the Lagrange multiplier method to the find the maximum R(p,q) of subject to the constraint 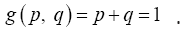 This is to solve the following system of equations:
This is to solve the following system of equations:
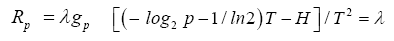
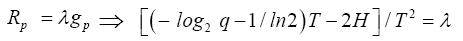
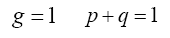
Equate the left-sides of the first two equations and simplify to get
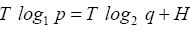
implying that 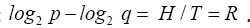 That is, at the maximal distribution (p,q) the maximal rate K2 is
That is, at the maximal distribution (p,q) the maximal rate K2 is
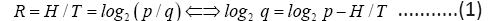
To find (p,q) we use the relation q=1-p from the constraint g(p,q)=1 the identity above to rewrite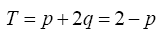 b and then to replace all q in H as follows
b and then to replace all q in H as follows
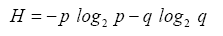
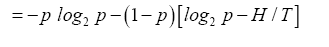
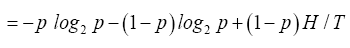
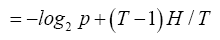
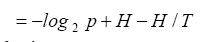
which is simplified to
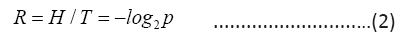
From Eq. (1) and Eq.(2) we have
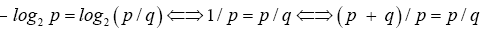
The last equality shows p/q is the Golden Ratio with
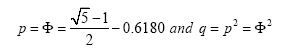
and the channel capacity is
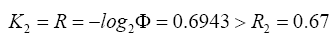
Better than the binary MTR.
In fact, this result is a special case of the following theorem which is a variation of Shannon’s result from [1]. A proof is a straightforward generalization of the Golden Ratio case above.
Theorem 1: For an n-alphabet communication system, its source transmission rate 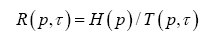 reaches a unique maximum
reaches a unique maximum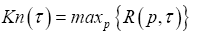 at an encoded source distribution P which is the solution to the following equations,
at an encoded source distribution P which is the solution to the following equations,
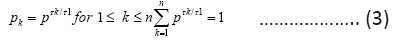 and the maximal rate (the channel capacity) is
and the maximal rate (the channel capacity) is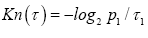
Proof. (For review only.) Since the maximization is independent from the base presenting time τ, we will drop all references of it from the function T and R. The proof is based on the Lagrange multiplier method to maximize R(P) subject to the constraint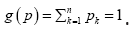 This is to solve the joint equations:
This is to solve the joint equations: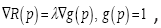 where ▼ is the gradient operator with respect to p and λ is the Lagrange multiplier. Denote
where ▼ is the gradient operator with respect to p and λ is the Lagrange multiplier. Denote 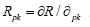 Then the first system of equations becomes
Then the first system of equations becomes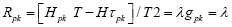 , component wise. Write out the partial derivatives of H and T and simplify, we have
, component wise. Write out the partial derivatives of H and T and simplify, we have 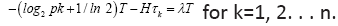 Subtract the equation for k=1 from each of the remaining n−1 equations to eliminate the multiplier λ and to get a set of n−1 new equations:
Subtract the equation for k=1 from each of the remaining n−1 equations to eliminate the multiplier λ and to get a set of n−1 new equations:
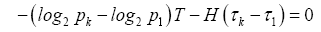
which solves to
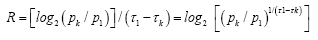
Introducing a new quantity 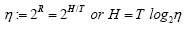 we can rewrite the equation above as
we can rewrite the equation above as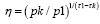 and equivalently
and equivalently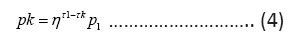
for all k. Next we express the entropy H in terms of η and p1, τ1, substituting out all pk :
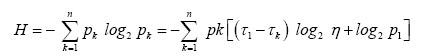
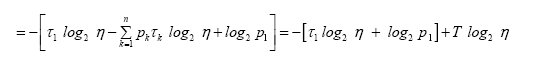
Where we have used 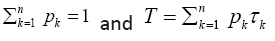 Since we have by definition
Since we have by definition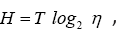 cancelling H from both sides of the equation above gives
cancelling H from both sides of the equation above gives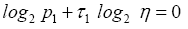 and consequently
and consequently
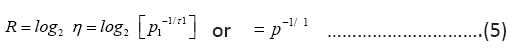 and from (4)
and from (4)

Last, solve the equation 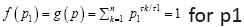 Since f (p1) is strictly increasing in p1 and f (0)=0 <1 and f(1)=n > 1, there is a unique solution
Since f (p1) is strictly increasing in p1 and f (0)=0 <1 and f(1)=n > 1, there is a unique solution By (5) and (6), the channel capacity is
By (5) and (6), the channel capacity is 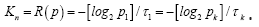 This completes the proof.
This completes the proof.
The Golden Ratio case is a corollary to the theorem with the assumption that τ2=2τ1 for n=2. And for the special case when τ2=kτ1 with n > 2, the CC distribution satisfies pk=pk1 for 1 ≤ k ≤ n with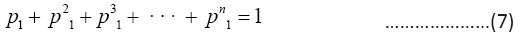
Denote the solution by 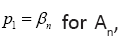 then we can easily show that βn is a decreasing sequence in n, converging to 0.5 and bounded exactly from above by the Golden ratio β2=Φ=0.6180.
then we can easily show that βn is a decreasing sequence in n, converging to 0.5 and bounded exactly from above by the Golden ratio β2=Φ=0.6180.
Multi-time scaled neuron model
In, a neuron model was discovered that remains symmetric under the conductance and resistance transformation: r=1/g and g=1/r [8]. The symmetry gives rise to the conductance characteristics for both ion channels and protein channels:
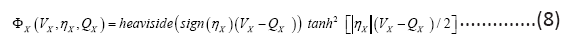
The model looks exactly the same under the transformation gr=1 and ψ=1/φ, the resistance characteristics, leading to a unique model for any given neuron, rather than innumerable ad hoc models as conventionally is the case. This model then predicts that the phenomenon of spontaneous firing of individual ion channels [9,10] by ways of quantum tunneling [11] is both sufficient and necessary, marking the first transition from the quantum realm to the microscopic world in neuronal modeling. The model automatically gives rise to different time scales for ion and protein channels, permitting dramatic simplifications in dimensional reduction. The model also clearly lays out a blueprint for circuit implementation by the channel characteristics (8). The model is capable of both action potential propagation and spike-burst generation. Here we consider a four channel neuron model:
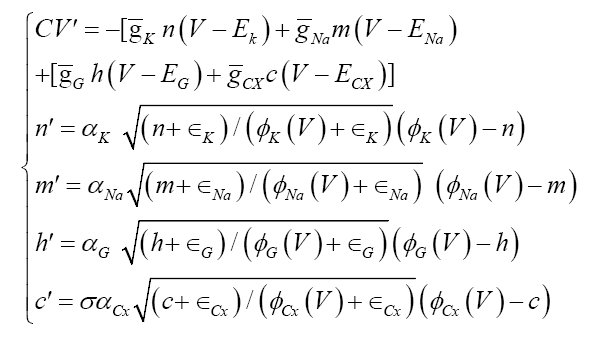
where Na is for the sodium channel, K is for the potassium channel, G is for the sodium-potassium gating channel, and the fourth channel, Cx, can be a calcium channel or a chlorine channel, or a protein channel, which are needed for spike-burst. Parameter σ takes only a fixed sign value, +1 or −1, because both can generate spike burst. Without the spontaneous firing parameters X, the model encounters a dividing-zero singularity and a flat-lining equilibrium, meaning the neuron are neither functional nor alive. All results outlined above are obtained in [8].
The rate parameters, αX, naturally make the model multi-time scaled. For example, the full 5-dimensional system (9) can be reduced to a 3-dimensional system below by assuming the gating and the sodium channels to be the fastest with αNa , αG sufficiently large so that m=φNa (V) and h=φG (V ):
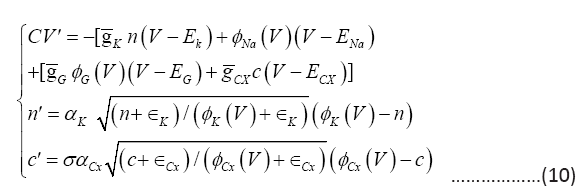
Simulations can be down on both with their dynamics indistinguishable for large αNa , αG System (10) is another multi-time system, with the V -equation fast, the n-equation slow or comparable, and the c-equation slower. The lower dimensional reduction (10) can be advantageous for analytical manipulations c.f. [12].
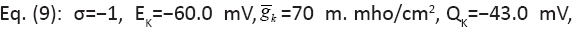
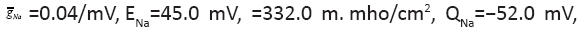
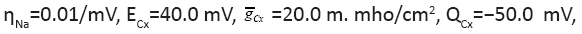
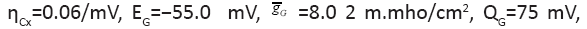
 The changing parameter is for
The changing parameter is for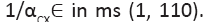 Quantitatively similar result also holds (not shown) for the same parameters except for
Quantitatively similar result also holds (not shown) for the same parameters except for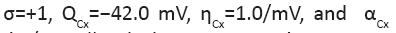 between 0.01/ms and 1/ms. All spike bursts start at the same initial values V (0)=−49, n(0)=m(0)=0, h(0)=1, and c(0)=0.025.
between 0.01/ms and 1/ms. All spike bursts start at the same initial values V (0)=−49, n(0)=m(0)=0, h(0)=1, and c(0)=0.025.
In Figures 1A and 1B, all parameters are fixed from except for the rate parameter αCx which is used as a bifurcation parameter. The plot is presented against 1/αCx for a better visibility [8]. From the graph we can conclude immediately that if we denote the first bifurcation of k spikes by αCx, k, then the sequence scales like the Harmonic sequence
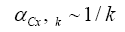
and its renormalization
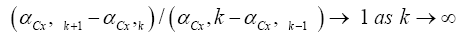
Converges to a universal number which is the first natural number 1, according to the neural spike renormalization theory of [13,14]. Second, the refractory time for the k-spike burst is proportional to the bursting time because their ratio is approximately a constant around 0.5, so that the kth spike base time τk for letter bk is approximately (1+0.5) × bursting time for bk. Thirdly, from the spike frequency plot we can conclude that it is approximately a constant around 1 cycle per msec for all spike bursts. As a result, the k-spike burst takes about k msec. All these values can be obtained by choosing an αCx value from the k-spike interval which is called the isospike interval. Hence, we can conclude empirically that (Figures 2A and 2B)
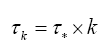
For some constant τ* around 1.5 msec. Hence, the hypothesis is satisfied for the information distribution equation (7) for the Golden Ratio distribution (n=2) and for the generalized Golden Ratio distribution (n > 2).
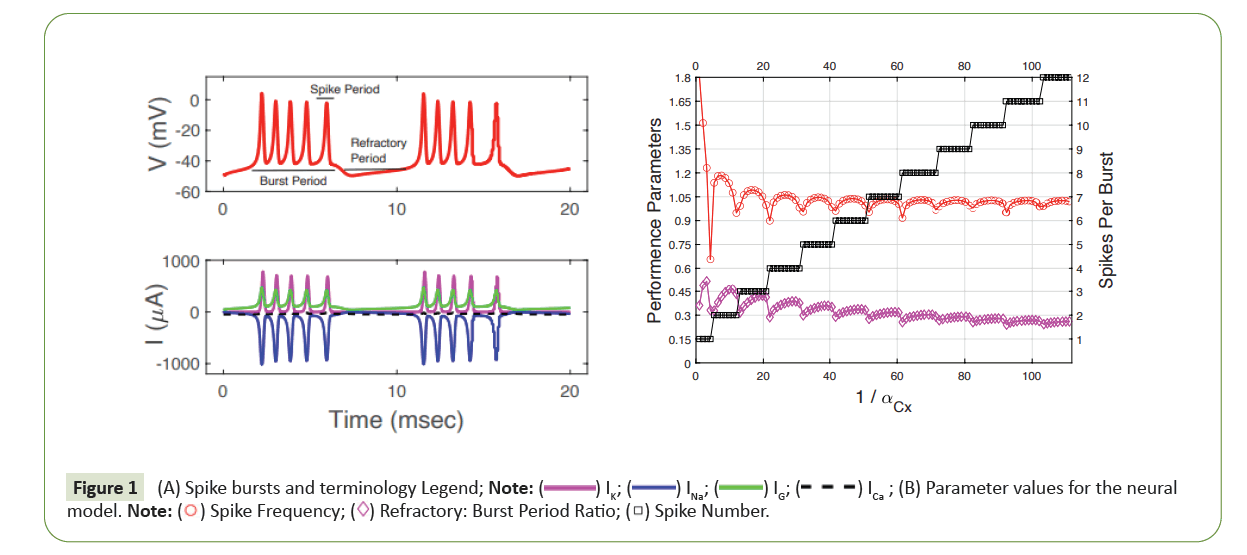
Figure 1: (A) Spike bursts and terminology Legend; Note: (B) Parameter values for the neural
(B) Parameter values for the neural
model.
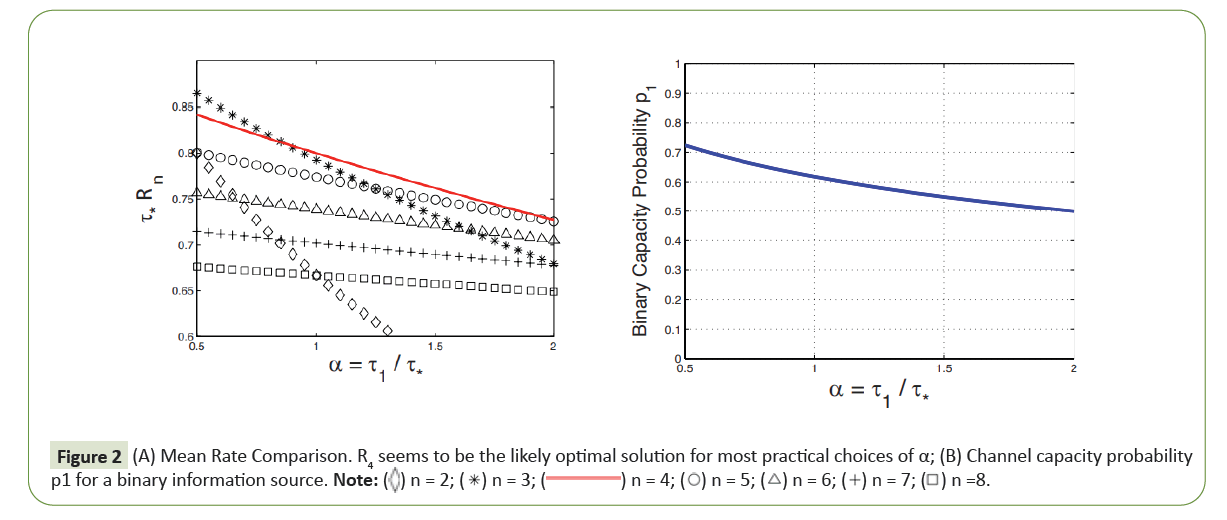
Figure 2: (A) Mean Rate Comparison. R4 seems to be the likely optimal solution for most practical choices of α; (B) Channel capacity probability p1 for a binary information source. 
Results and Discussion
From Figure 1A we can see that the 1-spike burst is different
from the rest. Although we can find parameter value from the
1-spike parameter interval to behave similarly to the rest of the spike bursts in the base process time τ1 but in practice, such a
value can be hard to fixed. Instead, its spike-frequency can be
higher or lower than the average of the rest. This is due to a
phenomenon, referred to as spike frequency adaptation [4,5], for
neural models. Let τ* be the same parameter as in (11) that is the average spike-burst period for k ≥ 2 and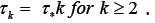 For the
1-spike burst, we express its processing time as a scalar multiple of
For the
1-spike burst, we express its processing time as a scalar multiple of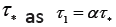 for some α either greater, or equal to, or smaller than 1. Thus, for the MTR, Rn, for the An code,
for some α either greater, or equal to, or smaller than 1. Thus, for the MTR, Rn, for the An code,
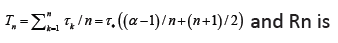
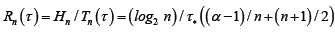
Figure 2A plots its graph against the parameter α. It shows for the
range of 0.5 < α < 2, the optimal MRT is with A3 or A4. For the
binary alphabet’s channel capacity, the optimal distribution for
the 1-spike burst is computed numerically from the equation (3):
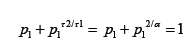
for each α from the interval (1/110, 1). Figure 2B shows the graph
of the solution as a function of α. It goes through the Golden
Ratio at α=1 as expected.
Obviously, nature has built a communication system out of
neurons. The results above suggest that such systems come with
inherent preferences in information. There are many examples of
memory related animal systems where the number of preferred
modes for operation is around 4 the so-called magic number 4
phenomena, c.f. [15-18]. The underlining hypothesis is that animal
brains have a neurological tendency to maximize information
entropy against time in cost. Information sources with the Golden
Ratio distribution are many. One example is the Golden Sequence,
101101011011010110101..., which is generated by starting with a
symbol 1 and iterating the sequence according to 2 rules: replace
every symbol 1 in the sequence by 10 and replace every symbol
0 in the sequence by 1. The distribution {p0, p1} of the symbols
{0, 1} along the sequence has the Golden Ratio distribution:
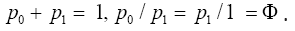 This gives a perfect illustration
of Shannon’s fundamental theory of noiseless channel; assigning
symbol 1 to the 1-spike burst base and symbol 0 to the 2-spike
burst base for the source-to-channel encoding gives rise to the
binary neural system’s channel capacity. Penrose’s aperiodic tiling
is another example with Golden Ratio distribution. In its simplest
form, its bases consist of a 54-degree rhombus and a 72-degree
rhombus. The frequencies with which the rhombi appear in the
plane follow the Golden Ratio distribution [19]. Again, a trivial
but most natural source-to-channel encoding gives rise to the
fastest source transmission rate for the binary neural code.
This gives a perfect illustration
of Shannon’s fundamental theory of noiseless channel; assigning
symbol 1 to the 1-spike burst base and symbol 0 to the 2-spike
burst base for the source-to-channel encoding gives rise to the
binary neural system’s channel capacity. Penrose’s aperiodic tiling
is another example with Golden Ratio distribution. In its simplest
form, its bases consist of a 54-degree rhombus and a 72-degree
rhombus. The frequencies with which the rhombi appear in the
plane follow the Golden Ratio distribution [19]. Again, a trivial
but most natural source-to-channel encoding gives rise to the
fastest source transmission rate for the binary neural code.
Equation (12) for α gives a way to quantify how close something is
to the Golden Ratio. For example, a rectangular frame is uniquely
defined by its height-to-width (aspect) ratio. A frame of the
Golden Ratio is 1:1.6180=1:1/Φ. To translate it into a statistical
distribution over a binary
source, both height and width need to be proportionated
against the height-width sum. Thus, the width: sum fraction is 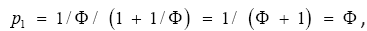 the Golden Ratio, which
in turn corresponds to α=1 if {p1, 1−p1} is the binary channel
capacity distribution. The aspect ratio of a typical wide-screen
monitor is 10:16, corresponding to a p1=16/26=0.6154 binary
distribution, and α ∼ 0.99 for the neural binary channel capacity.
The aspect ratio of a high definition TV is 9:16, corresponding to
a p1=16/25=0.64 binary distribution, or α ~ 0.90. All fall inside
the R4-optimal mean rate range and near the Golden Ratio
distribution for binary channel capacities as shown in Figure 2A.
the Golden Ratio, which
in turn corresponds to α=1 if {p1, 1−p1} is the binary channel
capacity distribution. The aspect ratio of a typical wide-screen
monitor is 10:16, corresponding to a p1=16/26=0.6154 binary
distribution, and α ∼ 0.99 for the neural binary channel capacity.
The aspect ratio of a high definition TV is 9:16, corresponding to
a p1=16/25=0.64 binary distribution, or α ~ 0.90. All fall inside
the R4-optimal mean rate range and near the Golden Ratio
distribution for binary channel capacities as shown in Figure 2A.
Conclusion
In conclusion, with the assumption that the number of spikes
per burst forms a letter of an alphabet and the processing times
for the letters progress like the natural number, then the neural
spike code with the first four letters achieves the best average
information rate, and for any binary source, the information
distribution in Golden Ratio achieves the binary channel capacity
for the neural spike code. Altogether, our result seems to support
the hypothesis that human’s brain is biologically build for
informational preferences.
Altogether, our result seems to support the hypothesis that
human’s brain is biologically build for informational preferences.
Declarations
Ethical approval
Not Applied.
Competing interests
None.
Authors’ contributions
Not Applied.
Funding
None.
Availability of data and materials
All data generated or analysed during this study are included
in this published article. Matlab mfiles are available from the
corresponding author on reasonable request.
References
- Shannon CE (1948) A mathematical theory of communication. Bell Syst tech j 27: 379-423 and 623-656.
[Crossref] [Google scholar]
- Rinzel JA (1985) A formal classification of bursting mechanisms in excitable systems. (1st edn) Berlin: Heidelberg: Springer,Germany.
[Google scholar]
- Terman D (1992) The transition from bursting to continuous spiking in excitable membrane models. J Nonlinear Sci 2:135-182.
[Google scholar]
- Guckenheimer J, Harris-Warrick R, Peck J (1997) Bifurcation, bursting, and spike frequency adaptation. J Comput Neurosci 4:257-277.
[Crossref] [Google scholar] [PubMed]
- Ermentrout B, Terman D (2010) Foundations of mathematical neuroscience. (1st edn) Berlin: Springer, Germany.
[Google scholar]
- Perkel DH, Bullock TH (1968) Neural coding. Neurosci Res Prog Sum 3:405-527.
- Reza FM (1994) An introduction to information theory. (1st edn) Kerala: Dover Publications, India.
- Deng B (2019) Neuron model with conductance-resistance symmetry. Phys Lett A 383:125976.
[Crossref] [Google scholar]
- Zagotta WN, Brainard MS, Aldrich RW (1988) Single-channel analysis of four distinct classes of potassium channels in Drosophila muscle. J Neurosci 8:4765-4779.
[Crossref] [Google scholar] [PubMed]
- Sakmann B (2013) Single-channel recording. (2nd edn) New York: Springer Science and Business Media, USA.
- Nawafleh S (2022) GABA receptors can depolarize the neuronal membrane potential via quantum tunneling of chloride ions: a quantum mathematical study. Cells 11:1145.
[Crossref] [Google scholar] [PubMed]
- Cheng F, Li J, Yu Q (2023) The existence of solitary wave solutions for the neuron model with conductance-resistance symmetry. AIMS Mathematics 8:3322-3337.
[Crossref] [Google scholar]
- Deng B (2011) Neural spike renormalization. Part I-Universal number1. J Diff Eq 250:2940-2957.
[Crossref] [Google scholar]
- Deng B (2011) Neural spike renormalization. Part II-Multiversal chaos. J Diff 250:2958-2968.
[Crossref] [Google scholar]
- Miller GA (1956) The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychol Rev 63:81-97.
[Crossref] [Google scholar]
- Boynton RM (1979) Human Color Vision, Holt, Rinehart and Winston. (2nd edn) New York: Wiley Online Library, USA.
- Pollack GD, Casseday JH (1989) The neural basis of echolaction in bats. (1st edn) Berlin: Srpinger-Verlage, Germany.
- Cowan N (2001) The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behav Brain Sci2 4:87-185.
[Crossref] [Google scholar] [PubMed]
- de Bruijn NG (1981) Algebraic theory of Penrose’s non-periodic tilings of the plane. Indag Math 43:38-66.
[Crossref] [Google scholar]
Citation: Deng B (2023) Golden Ratio Information for Neural Spike Code. J Neurol Neurosci Vol. 14 No.S7:001





 a source-to-channel encoding is a mapping from the source alphabet
a source-to-channel encoding is a mapping from the source alphabet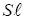 to the set of finite sequences of the system alphabet An so that a source sequence in
to the set of finite sequences of the system alphabet An so that a source sequence in 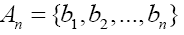
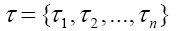
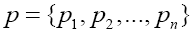
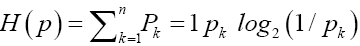
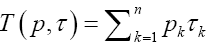
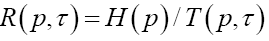
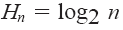
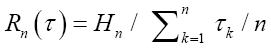
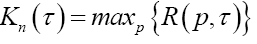
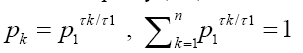
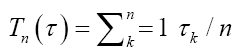 in time per base. Hence, the key performance parameter for an n-alphabet communication system is this payoff-to-cost ratio
in time per base. Hence, the key performance parameter for an n-alphabet communication system is this payoff-to-cost ratio 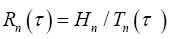 in bit per time, referred to as the Mean Transmission Rate (MTR) or the transmission rate for short. This is an intrinsic measure for all communication systems, regardless of the size nor the nature of their alphabets. As a result, different systems can be objectively compared. In the example of Internet, the transmission rate is the measure we use to compare different means of connection, such as coaxial cable, optic fiber or satellite. Notice also that the mean transmission rate is determined by all sources, and it is in this sense that the transmission rate is a passive measurement of a communication system.
in bit per time, referred to as the Mean Transmission Rate (MTR) or the transmission rate for short. This is an intrinsic measure for all communication systems, regardless of the size nor the nature of their alphabets. As a result, different systems can be objectively compared. In the example of Internet, the transmission rate is the measure we use to compare different means of connection, such as coaxial cable, optic fiber or satellite. Notice also that the mean transmission rate is determined by all sources, and it is in this sense that the transmission rate is a passive measurement of a communication system. 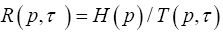 with p being its distribution over the system alphabet An This rate may be faster or slower than the mean rate Rn(p,τ). is no worse than the mean. The mathematical problem is to maximize the source transmission rate Rn(p,τ) over all choices of the distribution p. Solution to the optimization problem gives rise to the channel capacity (CC), denoted by Kn.
with p being its distribution over the system alphabet An This rate may be faster or slower than the mean rate Rn(p,τ). is no worse than the mean. The mathematical problem is to maximize the source transmission rate Rn(p,τ) over all choices of the distribution p. Solution to the optimization problem gives rise to the channel capacity (CC), denoted by Kn.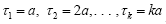 for code base
for code base 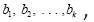 respectively, for a fixed parameter a. That is, the 1-spike base takes 1 unit of time in a to process; the 2-spike base takes 2 units of time in 2a to process and so on. Without loss of generality we can drop a by assuming a=1 for now.
respectively, for a fixed parameter a. That is, the 1-spike base takes 1 unit of time in a to process; the 2-spike base takes 2 units of time in 2a to process and so on. Without loss of generality we can drop a by assuming a=1 for now.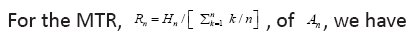
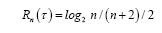
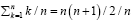 For
For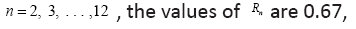 0.79, 0.80, 0.77, 0.74, 0.70, 0.67, 0.63, 0.60, 0.58, 0.55
0.79, 0.80, 0.77, 0.74, 0.70, 0.67, 0.63, 0.60, 0.58, 0.55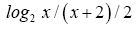 is a decreasing function for × > 4.
is a decreasing function for × > 4. 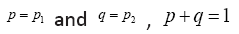 Then
Then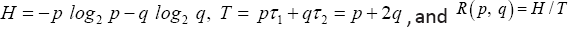 . We use the Lagrange multiplier method to the find the maximum R(p,q) of subject to the constraint
. We use the Lagrange multiplier method to the find the maximum R(p,q) of subject to the constraint 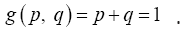 This is to solve the following system of equations:
This is to solve the following system of equations: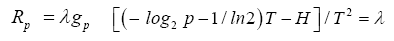
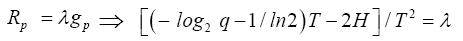
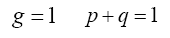
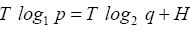
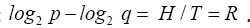 That is, at the maximal distribution (p,q) the maximal rate K2 is
That is, at the maximal distribution (p,q) the maximal rate K2 is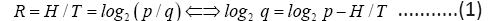
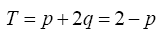 b and then to replace all q in H as follows
b and then to replace all q in H as follows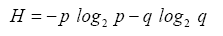
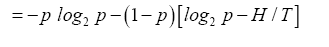
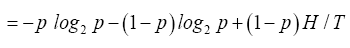
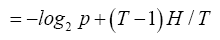
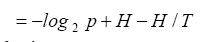
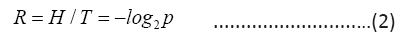
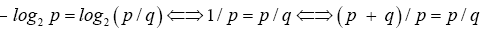
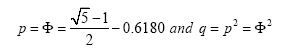
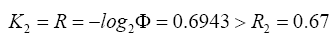
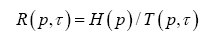 reaches a unique maximum
reaches a unique maximum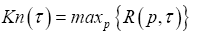 at an encoded source distribution P which is the solution to the following equations,
at an encoded source distribution P which is the solution to the following equations,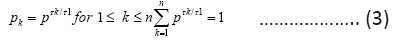 and the maximal rate (the channel capacity) is
and the maximal rate (the channel capacity) is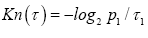
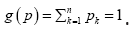 This is to solve the joint equations:
This is to solve the joint equations: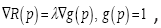 where ▼ is the gradient operator with respect to p and λ is the Lagrange multiplier. Denote
where ▼ is the gradient operator with respect to p and λ is the Lagrange multiplier. Denote 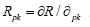 Then the first system of equations becomes
Then the first system of equations becomes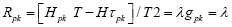 , component wise. Write out the partial derivatives of H and T and simplify, we have
, component wise. Write out the partial derivatives of H and T and simplify, we have 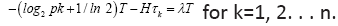 Subtract the equation for k=1 from each of the remaining n−1 equations to eliminate the multiplier λ and to get a set of n−1 new equations:
Subtract the equation for k=1 from each of the remaining n−1 equations to eliminate the multiplier λ and to get a set of n−1 new equations: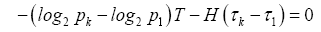
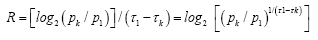
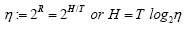 we can rewrite the equation above as
we can rewrite the equation above as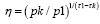 and equivalently
and equivalently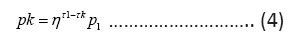
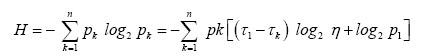
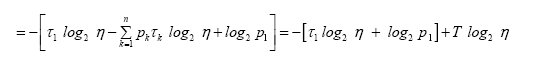
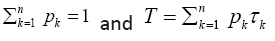 Since we have by definition
Since we have by definition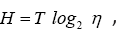 cancelling H from both sides of the equation above gives
cancelling H from both sides of the equation above gives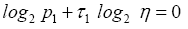 and consequently
and consequently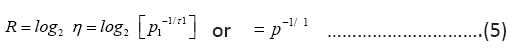 and from (4)
and from (4)
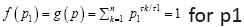 Since f (p1) is strictly increasing in p1 and f (0)=0 <1 and f(1)=n > 1, there is a unique solution
Since f (p1) is strictly increasing in p1 and f (0)=0 <1 and f(1)=n > 1, there is a unique solution By (5) and (6), the channel capacity is
By (5) and (6), the channel capacity is 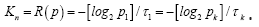 This completes the proof.
This completes the proof. 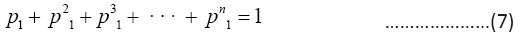
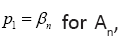 then we can easily show that βn is a decreasing sequence in n, converging to 0.5 and bounded exactly from above by the Golden ratio β2=Φ=0.6180.
then we can easily show that βn is a decreasing sequence in n, converging to 0.5 and bounded exactly from above by the Golden ratio β2=Φ=0.6180.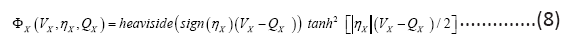
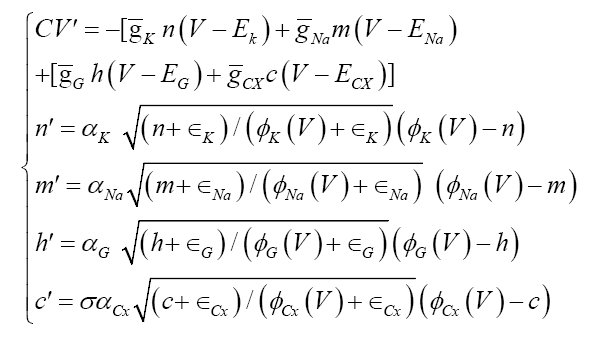
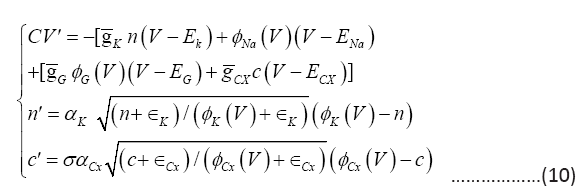
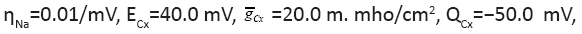
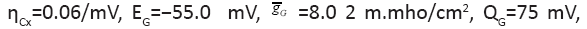
 The changing parameter is for
The changing parameter is for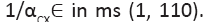 Quantitatively similar result also holds (not shown) for the same parameters except for
Quantitatively similar result also holds (not shown) for the same parameters except for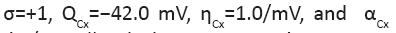 between 0.01/ms and 1/ms. All spike bursts start at the same initial values V (0)=−49, n(0)=m(0)=0, h(0)=1, and c(0)=0.025.
between 0.01/ms and 1/ms. All spike bursts start at the same initial values V (0)=−49, n(0)=m(0)=0, h(0)=1, and c(0)=0.025.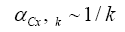
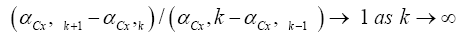
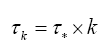

 (B) Parameter values for the neural
(B) Parameter values for the neural

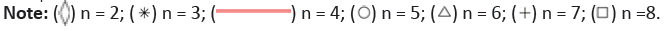
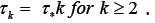 For the
1-spike burst, we express its processing time as a scalar multiple of
For the
1-spike burst, we express its processing time as a scalar multiple of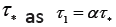 for some α either greater, or equal to, or smaller than 1. Thus, for the MTR, Rn, for the An code,
for some α either greater, or equal to, or smaller than 1. Thus, for the MTR, Rn, for the An code,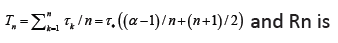
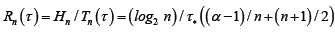
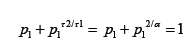
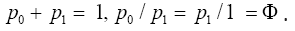 This gives a perfect illustration
of Shannon’s fundamental theory of noiseless channel; assigning
symbol 1 to the 1-spike burst base and symbol 0 to the 2-spike
burst base for the source-to-channel encoding gives rise to the
binary neural system’s channel capacity. Penrose’s aperiodic tiling
is another example with Golden Ratio distribution. In its simplest
form, its bases consist of a 54-degree rhombus and a 72-degree
rhombus. The frequencies with which the rhombi appear in the
plane follow the Golden Ratio distribution [
This gives a perfect illustration
of Shannon’s fundamental theory of noiseless channel; assigning
symbol 1 to the 1-spike burst base and symbol 0 to the 2-spike
burst base for the source-to-channel encoding gives rise to the
binary neural system’s channel capacity. Penrose’s aperiodic tiling
is another example with Golden Ratio distribution. In its simplest
form, its bases consist of a 54-degree rhombus and a 72-degree
rhombus. The frequencies with which the rhombi appear in the
plane follow the Golden Ratio distribution [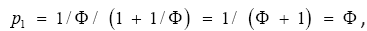 the Golden Ratio, which
in turn corresponds to α=1 if {p1, 1−p1} is the binary channel
capacity distribution. The aspect ratio of a typical wide-screen
monitor is 10:16, corresponding to a p1=16/26=0.6154 binary
distribution, and α ∼ 0.99 for the neural binary channel capacity.
The aspect ratio of a high definition TV is 9:16, corresponding to
a p1=16/25=0.64 binary distribution, or α ~ 0.90. All fall inside
the R4-optimal mean rate range and near the Golden Ratio
distribution for binary channel capacities as shown in Figure 2A.
the Golden Ratio, which
in turn corresponds to α=1 if {p1, 1−p1} is the binary channel
capacity distribution. The aspect ratio of a typical wide-screen
monitor is 10:16, corresponding to a p1=16/26=0.6154 binary
distribution, and α ∼ 0.99 for the neural binary channel capacity.
The aspect ratio of a high definition TV is 9:16, corresponding to
a p1=16/25=0.64 binary distribution, or α ~ 0.90. All fall inside
the R4-optimal mean rate range and near the Golden Ratio
distribution for binary channel capacities as shown in Figure 2A.